Traditional Floating point conversion in C and assembler

Author: Andre Adrian
Date: 2025-04-20

Introduction

The book "Microprocessor programming for computer hobbyists" by Neill Graham from 1977 describes the traditional microprocessor approach for radix conversion. The traditional approach uses multiple multiplication or division instead of mantissa multiplication table and exponent constant table.
I wrote radix 10 to radix 2 and vice versa conversion in C. Inspiration was from the Graham book, but execution was myself. Pick the grain, leave the chaff is the idea.
Different C compilers have different floating point implementations. I tested three different CPUs: The HI-TECH Z80 CP/M C compiler V3.09. The Zilog Z80 CPU was in my Sinclair ZX81 and Spectrum home computers. Next C compiler is Alcyon C 1.3 for CP/M 68K. The Motorola 68000 was in my Atari ST computer. Last but not least is gcc, the GNU C compiler for my 64bit MS-Windows with a Intel 80386 style CPU, exactly AMD Ryzen 3300X.

Boring stuff

We could start with reading mantissa (fraction) as string of ASCII characters with an optional sign character and an optional decimal point "somewhere". But this is boring. Therefore we only use positive integer as mantissa and start our algorithms with mantissa as unsigned long value and exponent as signed int value. Stop writing string parsing routines, start writing algorithms!

Download

The original software development is repeated in some "development snapshots". Here is the C source code tfpconv.zip.

Radix 10 to radix 2, positive exponent

A bright idea in the traditional radix conversion is to treat the mantissa as integer number. We can express the mantissa always as integer. The floating point number 1.234567 can be written as 1234567*10^-6. I use 24 bits for mantissa. The maximum 24 bit unsigned integer is 16777215 or 0xFFFFFF. We can express the 7 digit decimal number 9999999 with these 24 bits.

As first example we convert 9999999*10^0 decimal to binary. The traditional algorithm for positive radix 10 exponent first tries to decrease the radix 10 exponent. If not possible the radix 2 exponent is increased. The idea is simple: Decrease the radix 10 exponent, increase the radix 2 exponent until the radix 10 exponent is zero. Changing the exponent changes the mantissa, too. Decreasing the radix 10 exponent by 1 needs mantissa multiplication by 10 to compensate. Increasing the radix 2 exponent by 1 needs mantissa division by 2 to compensate.

The constant Max10 is the maximum number that allows multiplication by 10 without overflow. We use 32 bit registers on the Motorola 68000 CPU. With a 24 bit mantissa, 8 bits are "spare" for guard bits. All guard bits are trailing bits. Before the "real" algorithm, the guard bits with value zero are appended to the mantissa bits. After the "real" algorithm, we add Round, that is a scaled 0.5 value. This allows rounding by truncation.

The C language keyword "register" tells the C compiler to put variables into registers. There is no memory address for these register variables, but execution is faster. The CP/M 68K Alcyon C can put per function five 32bit variables in registers and three pointers in registers. Modern C compilers do automatic register allocation and ignore the register keyword. The Alcyon C compiler can not handle initialized local array variables. Therefore m10[] and e10[] are static.

The Hi-Tech C compiler for Z80 CPU allows only K&R style comments /* */. This compiler has a problem with unsigned long compare "while(m <= Max10)". See interlude below for a workaround.

The mantissa value 0 is a special case and forces an early return.

/* a2f.c */ #include <stdio.h> #define Guard 8 #define Round 128 #define Max10 0x19999999L unsigned long asc2fp(e2_, m, e10) /* out: radix 2 mantissa */ int *e2_; /* out: radix 2 exponent */ register unsigned long m; /* in: mantissa */ register int e10; /* in: radix 10 exponent */ { register int e2 = 0; printf(" %8luE%d\n", m, e10); if (0 == m) { *e2_ = 0; return 0; } m <<= Guard; printf(" %2d %8lu*2^%d 0x%08lx \n", e10, m>>8, e2, m); if (e10 > 0) { for(;;) { while (m <= Max10) { m *= 10; --e10; printf("*10 %2d %8lu*2^%d 0x%08lx \n", e10, m>>8, e2, m); } if (e10 <= 0) break; while (m > Max10) { m /= 2; ++e2; printf("/2 %2d %8lu*2^%d 0x%08lx \n", e10, m>>8, e2, m); } } } m >>= 1; /* avoid 0xfffffff0 problem */ m += 64; m >>= 7; *e2_ = e2; printf(" %8lu*2^%d\n", m, e2); return m; } int main() { /* radix 10 mantissa m10, radix 10 exponent e10 */ static unsigned long m10[] = {9999999L, 9999999L, 9999999L}; static int e10[] = {0, 1, 2}; int i; for (i = 0; i < 3; ++i) { int e2; unsigned long m2 = asc2fp(&e2, m10[i], e10[i]); printf("\n"); } } The program converts the three numbers 9999999*10^0, 9999999*10^1 and 9999999*10^2. The mantissas are "normalized", that is the mantissa value is between Max10 and 2^24-1, the maximum unsigned 24bit value. Normalized numbers have the best accuracy (precision).

The first number is easy. A normalized mantissa needs no mantissa processing and the exponent 10^0 is 1, as is the exponent 2^0. The mantissa goes "in", guard bits are appended and removed and the same mantissa goes "out":

9999999E0 0 9999999*2^0 0x98967f00 9999999*2^0 The second number needs some mantissa division by two before the mantissa is below Max10 and multiplication by 10 is possible. The first column is the radix 10 exponent. Next column is ASCII representation of floating point number. The last column is mantissa as hexadecimal number.

Note: one multiply by 10 is compensated by 3 to 4 divide by 2, that is divide by 8 or divide by 16. The algorithm approximates the ratio log(10)/log(2) = 3.3219... with 3 or 4 divides by 2.

9999999E1 1 9999999*2^0 0x98967f00 /2 1 4999999*2^1 0x4c4b3f80 /2 1 2499999*2^2 0x26259fc0 /2 1 1249999*2^3 0x1312cfe0 *10 0 12499998*2^3 0xbebc1ec0 12499999*2^3
The third number needs more multiply by 10 and divide by 2. This is the disadvantage of the traditional algorithm: larger exponents need more mantissa operations (multiply or divide). Every operation looses a little accuracy. Our 8 guard bits are not enough to get every time the same number back after conversion to radix 2 and back to radix 10. The maximum error is one bit. The result 15624998*2^6 evaluates to 999999872, but it should be 999999900.

9999999E2 2 9999999*2^0 0x98967f00 /2 2 4999999*2^1 0x4c4b3f80 /2 2 2499999*2^2 0x26259fc0 /2 2 1249999*2^3 0x1312cfe0 *10 1 12499998*2^3 0xbebc1ec0 /2 1 6249999*2^4 0x5f5e0f60 /2 1 3124999*2^5 0x2faf07b0 /2 1 1562499*2^6 0x17d783d8 *10 0 15624998*2^6 0xee6b2670 15624998*2^6

Interlude: Long compare

The Hi-Tech C compiler has a problem with unsigned long compare, e.g. "while(m <= Max10)". A long compare can be done with some short compares. The constant Max10 is split into two constants Max10H and Max10L for higher 16bits and lower 16bits.
The test program has a unsigned long compare in the first for loop. This single long compare is replaced by some short compares in the second for loop.

/* tlcmp.c */ #include <stdio.h> #define Max10 0x19999999L #define Max10H 0x1999 #define Max10L 0x9999 typedef union { unsigned long l; unsigned short s[2]; } UL; int main() { static unsigned long m10[] = { 0x19980000L, 0x19999998L, 0x19999999L, 0x199A0000L, 0x1999999AL, 0x80000000L, 0xFFFFFFFFL}; int i; for (i = 0; i < 7; ++i) { if (m10[i] <= Max10) { printf(" yes"); } else { printf(" no "); } } printf("\n"); for (i = 0; i < 7; ++i) { UL m; m.l = m10[i]; if (m.s[1] < Max10H || (m.s[1] == Max10H && m.s[0] <= Max10L)) { printf(" yes"); } else { printf(" no "); } } printf("\n"); }

The output of gcc C compiler is correct for both kinds of compare:

yes yes yes no no no no yes yes yes no no no no

The output of Hi-Tech C compiler is wrong for long compare with values having the most significant bit set:

Interlude: Division by 10.0

To convert negative radix 10 exponent, the algorithm increases the radix 10 exponent by one and divides the mantissa by 10 to compensate. Our division by 10 is a 32bit / 32 bit operation. Unfortunately, the CP/M 68K Alcyon C compiler has a bug. I assume, it can only do 32bit / 16bit operation. Therefore I wrote a div10() function. The first version is a direct coding of "division by hand".

We calculate q = n / d with d=10. We assume a normalized integer n, this is most significant bit is set. Therefore d is "left justified". The core operation is "subtract the shifted divisor from the dividend conditionally". The condition is dividend is larger or equal to shifted divisor. The variable qm is the "quotient mask", or the "current bit position for the condition result".

The divisor is shifted until the value 10 is "right justified". This takes 29 shifts. This is one of these "+/-1 errors". The register has 32bits, the radix 2 representation of 10 has 4 bits, therefore 28 shifts look correct, but are wrong.

/* div10.c */ #include <stdio.h> unsigned long div10(n) /* out: quotient */ register unsigned long n; /* in: nominator */ { register unsigned long d = 0xA0000000L; register unsigned long qm = 0x10000000L; register unsigned long q = 0L; register int i; printf("0x%08lx 0x%08lx 0x%08lx 0x%08lx\n", n, d, qm, q); for (i = 0; i < 29; ++i) { if (n >= d) { n -= d; q |= qm; } printf("0x%08lx 0x%08lx 0x%08lx 0x%08lx\n", n, d, qm, q); d >>= 1; qm >>= 1; } return q; } int main() { unsigned long q = div10(0xFFFFFFFFL); printf("0x%08lx /10= 0x%08lx\n", 0xFFFFFFFFL, q); }

The program output shows the bit-for-bit operation of div10. We see that one bit in variable qm moves from left to right and that the four bits "1010" in variable d move left to right, too. The value of n decreases, the value of q increases. After the algorithm finished, variable n contains the division remainder.

n d qm q 0xffffffff 0xa0000000 0x10000000 0x00000000 0x5fffffff 0xa0000000 0x10000000 0x10000000 0x0fffffff 0x50000000 0x08000000 0x18000000 0x0fffffff 0x28000000 0x04000000 0x18000000 0x0fffffff 0x14000000 0x02000000 0x18000000 0x05ffffff 0x0a000000 0x01000000 0x19000000 0x00ffffff 0x05000000 0x00800000 0x19800000 0x00ffffff 0x02800000 0x00400000 0x19800000 0x00ffffff 0x01400000 0x00200000 0x19800000 0x005fffff 0x00a00000 0x00100000 0x19900000 0x000fffff 0x00500000 0x00080000 0x19980000 0x000fffff 0x00280000 0x00040000 0x19980000 0x000fffff 0x00140000 0x00020000 0x19980000 0x0005ffff 0x000a0000 0x00010000 0x19990000 0x0000ffff 0x00050000 0x00008000 0x19998000 0x0000ffff 0x00028000 0x00004000 0x19998000 0x0000ffff 0x00014000 0x00002000 0x19998000 0x00005fff 0x0000a000 0x00001000 0x19999000 0x00000fff 0x00005000 0x00000800 0x19999800 0x00000fff 0x00002800 0x00000400 0x19999800 0x00000fff 0x00001400 0x00000200 0x19999800 0x000005ff 0x00000a00 0x00000100 0x19999900 0x000000ff 0x00000500 0x00000080 0x19999980 0x000000ff 0x00000280 0x00000040 0x19999980 0x000000ff 0x00000140 0x00000020 0x19999980 0x0000005f 0x000000a0 0x00000010 0x19999990 0x0000000f 0x00000050 0x00000008 0x19999998 0x0000000f 0x00000028 0x00000004 0x19999998 0x0000000f 0x00000014 0x00000002 0x19999998 0x00000005 0x0000000a 0x00000001 0x19999999 0xffffffff /10= 0x19999999

The optimized division algorithm does not need the variable qm. If we shift the quotient left, we can append the current quotient bit at the least significant bit position. The loop exit is between the subtraction part and the shift part of the algorithm. After we have processed the last quotient bit, shifting q is an error.

/* div10a.c */ #include <stdio.h> unsigned long div10(n) /* out: quotient */ register unsigned long n; /* in: nominator */ { register unsigned long d = 0xA0000000L; register unsigned long q = 0L; register int i = 29; printf("0x%08lx 0x%08lx 0x%08lx\n", n, d, q); for (;;) { if (n >= d) { n -= d; q |= 1; } printf("0x%08lx 0x%08lx 0x%08lx\n", n, d, q); if (--i <= 0) break; d >>= 1; q <<= 1; } return q; } int main() { unsigned long q = div10(0xFFFFFFFFL); printf("0x%08lx /10= 0x%08lx\n", 0xFFFFFFFFL, q); }

The trace of optimized div10() looks different, because the quotient q "grows" from right to left. I assume, the optimized division algorithm is from the 1940s or earlier. The early computers like the IAS computer with multiplication and division hardware had only one accumulator register AC and one MQ register. The divisor value was taken from memory.

n, AC      d, Mem     q, MQ 0xffffffff 0xa0000000 0x00000000 0x5fffffff 0xa0000000 0x00000001 0x0fffffff 0x50000000 0x00000003 0x0fffffff 0x28000000 0x00000006 0x0fffffff 0x14000000 0x0000000c 0x05ffffff 0x0a000000 0x00000019 0x00ffffff 0x05000000 0x00000033 0x00ffffff 0x02800000 0x00000066 0x00ffffff 0x01400000 0x000000cc 0x005fffff 0x00a00000 0x00000199 0x000fffff 0x00500000 0x00000333 0x000fffff 0x00280000 0x00000666 0x000fffff 0x00140000 0x00000ccc 0x0005ffff 0x000a0000 0x00001999 0x0000ffff 0x00050000 0x00003333 0x0000ffff 0x00028000 0x00006666 0x0000ffff 0x00014000 0x0000cccc 0x00005fff 0x0000a000 0x00019999 0x00000fff 0x00005000 0x00033333 0x00000fff 0x00002800 0x00066666 0x00000fff 0x00001400 0x000ccccc 0x000005ff 0x00000a00 0x00199999 0x000000ff 0x00000500 0x00333333 0x000000ff 0x00000280 0x00666666 0x000000ff 0x00000140 0x00cccccc 0x0000005f 0x000000a0 0x01999999 0x0000000f 0x00000050 0x03333333 0x0000000f 0x00000028 0x06666666 0x0000000f 0x00000014 0x0ccccccc 0x00000005 0x0000000a 0x19999999 0xffffffff /10= 0x19999999
The programming language C has no carry flag. The carry flag is used in assembler programs to e.g. build 32bit addition out of multiple 8bit adds or 16bit adds. We can simulate carry flag in C and can write C source code that is very close to assembler:

/* div10b.c */ unsigned long div10(n)          /* out: quotient */     register unsigned long n;   /* in: nominator */ {     register char i = 29;     register unsigned long q = 0L;     register unsigned long d = 0xA0000000L;     printf("0x%08lx 0x%08lx 0x%08lx\n", n, d, q);     do {         char carry = n < d;         n -= d;         if (carry) {             n += d;         }         carry = !carry;         q <<= 1; q |= carry;         d >>= 1;         printf("0x%08lx 0x%08lx 0x%08lx %d\n", n, d, q, carry);     } while (--i > 0);     return q; }
To simulate the carry flag, we store the result of compare n < d in variable carry. An assembler subtraction opcode sets or clears the carry flag as side effect.
Note: The result of "n < d" is zero or one. This is implementation specific. Result could be zero or minus one.

After solving the div10 problem, I wanted to know: what is the problem exactly? Therefore I wrote a little test program.

/* tdiv10.c */ #include <stdio.h> int main() {     unsigned long m = 0xFFFFFFFL;     int i;     for(i = 0; i < 5; ++i) {         unsigned long m_ = m;         m_ /= 10;   /* test this operation */         printf("0x%08lx /10= 0x%08lx\n", m, m_);         m <<= 1;         m += 1;     } } The output on my MS-Windows computer with gcc C compiler is:

0x0fffffff /10= 0x01999999 0x1fffffff /10= 0x03333333 0x3fffffff /10= 0x06666666 0x7fffffff /10= 0x0ccccccc 0xffffffff /10= 0x19999999 The output on my 68k-MBC with Alycon C compiler is:

0x0FFFFFFF /10= 0x01999999 0x1FFFFFFF /10= 0x03333333 0x3FFFFFFF /10= 0x06666666 0x7FFFFFFF /10= 0x0CCCCCCC 0xFFFFFFFF /10= 0x0000FFFF The exact problem is with most significant nominator bit. The Alcyon C compiler can correctly do a 31 bit division. At this time I got an idea: split the div 10 into a div 2 and a div 5. The div 2 can be done by shift right one bit. If the Alcyon C compiler can do correct shift right of unsigned long, everything should be fine. The new test program is:

/* tdiv10a.c */ #include <stdio.h> int main() {     unsigned long m = 0xFFFFFFFL;     int i;     for(i = 0; i < 5; ++i) {         unsigned long m_ = m;         m_ >>= 1; m_ /= 5;   /* test this operation */         printf("0x%08lx /10= 0x%08lx\n", m, m_);         m <<= 1;         m += 1;     } } And bingo, the Alcyon C compiler produces the correct output. This is a simple example of "after you found the first solution, look for a second solution". Sometimes a second solution is VERY necessary, sometimes a second solution is nice to have.
In our case, the div10() function is 4% faster with Alcyon C then shift right one bit and div 5.

Z80 assembler division by 10.0

The Z80 has an alternate register set, this is a big improvement over Intel 8080 or Intel 8085. Next to registers A, B, C, D, E, H and L you have A', B', C', D', E', H' and L' from the alternate set. The opcode "exx" switches registers B to L between normal and alternate set. The opcode "ex af,af'" switches register A and flags (carry, zero, overflow, ...).
For optimized div10 we need three 32bit variables and one 8bit counter. The Z80 has enough registers for the job. The following Z80 assembler listing has language C comments. The assembler algorithm uses the carry flag, but there is no carry flag in the language C.
Let's start with the "test driver":

; test uldiv10 tuldiv10: exx ld hl,0FFFFh ; h'l'hl = 0xFFFFFFFF; exx ld hl,0FFFFh call uldiv10 halt

A comment starts with the character ;. The label tuldiv10: is the entry point of the test driver, the opcode halt is the exit point. The test driver loads the value 0xFFFFFFFF into the registers and calls the uldiv10 subroutine. The registers H and L can be used as a limited 16bit accumulator. You can add 16bit values to register pair HL and you can subtract 16bit values. The register A is the 8bit accumulator.
I present the uldiv10 subroutine in parts. The full assembler listing is in the Zip file. See section download above.

;================================================== ; H'L'HL = H'L'HL / 10 ; CHANGES D'E'DE, B'C'BC, A, Flags ; ;unsigned long div10(n) /* out: quotient */ ; register unsigned long n; /* in: nominator */ uldiv10: ;{ ld b,29 ; register char i = 29; xor a ; register unsigned long q = 0L; ld c,a ld d,a ; register unsigned long d = 0xA0000000L; ld e,a exx ld b,a ld c,a ld de,0A000h exx ; B'C'AC = H'L'HL / D'E'DE

The opcode "xor a" loads value zero in register A. The variable d uses the registers D'E'DE. In this notation, the leftmost register contains the most significant byte. The variable q uses the registers B'C'AC. Using these registers instead of B'C'BC saves a little program space and a little execution time. See details below. The variable i uses register B. Only register A' is not used.

dvloop: ; do { or a ; carry = n < d; n -= d; sbc hl,de exx sbc hl,de exx

The assembler program does not need a compare before the subtraction. Because there is no "sub hl,de" opcode, we clear the carry flag with opcode "or a". Then "sbc hl,de" behaves like "sub hl,de".

jr nc,endif ; if (carry) { add hl,de ; n += d; exx adc hl,de exx endif: ; }

The subtraction will set the carry flag, if n is smaller then d. The "jr nc,endif" opcode jumps to label endif: when carry was not set. This is the "jump away" logic of translating a C language if into assembler language. The if part "undos" the subtraction with an addition.

ccf ; carry = !carry; rl c ; q <<= 1; q |= carry; rla exx rl c rl b srl d ; d >>= 1; rr e exx rr d rr e

The carry flag is used as new quotient (result) bit. If the subtraction was without carry, that is successful, we shift a 1 bit into result. The variable q or registers B'C'AC and carry flag are shifted left one bit. The register A shift and rotate opcodes like "rla" are one byte, the other shift and rotate opcodes are two bytes. This is a little program code saving. The variable d or registers D'E'DE are shifted right one bit. The Z80 has shift and rotate opcodes for every register. The Intel 8080 and 8085 can only shift and rotate register A.

djnz dvloop ; } while (--i > 0);

The "do while" loop terminates at the bottom.

ld l,c ; return q; ld h,a exx ld l,c ld h,b exx ret ;}

The return value is expected in registers H'L'HL. Some load and exx opcodes do the job. Final opcode is return from subroutine. See file a2f6.as in the Zip file for full assembler code.

From 1976 on the MOS Technology 6502 and the Zilog Z80 were the prominent 8bit CPUs. In the early days, the 6502 was cheaper, but later the price was equal. In my opinion, the Z80 is much better in 32bit arithmetic. The 6502 has benefits for "shared video memory" home computers. The MSX Z80 home computers have Z80 with separate video memory. The Commodore C64 has 6502 with shared video memory.
Don't let the clock speeds fool you. A 1 MHz 6502 is as fast as a 2.5 MHz Z80.

6502 assembler division by 10.0

Division by 10.0 for mantissa can be done as multiplication by 0.1. Multiplication is faster then division and has no corner cases. The mantissa is a Q 0.32 number: zero bit before the binary point, 32 bits after the binary point.

; div10.65s ; unsigned 32bit mantissa divide by 10.0 as multiply by 0.1 ;-------------------------------- ulac = 0 ; unsigned long in: ac ulmq = ulac+4 ; unsigned long out: mq = ac * 0.1 ;-------------------------------- div10: ldy #33 ; Y = loop counter lda ulac ; A = ulac tax ; X = ulac bra .strt .do1 ; do { ror ulmq+3 ; ulmq >>= 1; ror ulmq+2 ror ulmq+1 ror ulmq lsr ulac+3 ; ulac >>= 1; ror ulac+2 ror ulac+1 txa ror tax .strt lsr ; ulac >>= 1; if (carry) { bcc .endi1 clc ; ulmq += 0.1; lda ulmq ; 0.1 = 0x1999999A as Q 0.32 number adc #$9A sta ulmq lda ulmq+1 adc #$99 sta ulmq+1 lda ulmq+2 adc #$99 sta ulmq+2 lda ulmq+3 adc #$19 sta ulmq+3 .endi1 ; } dey ; } while (--cnt); bne .do1 rts

The 6502 has only three 8-bit registers and the div10 subroutine uses all of them. The subroutine input and output is through memory locations in zero page, the address range from 0x0000 to 0x00FF. This is FORTRAN style non recursive parameter passing. CPU registers are fast, memory is slow and zero page memory is in between.
The 32bit accumulator AC starts at memory location ulac. The 32bit register MQ starts at memory location ulmq. The names AC and MQ go back to the multiply and divide unit of the IAS computer from 1948.
I use the 6502 Macroassembler & Simulator by Michal Kowalski as editor/assembler/simulator.

6502 assembler multiplication by 10

The multiplication by 10 is done with shifts and add.

; mul10.65s ; unsigned 32bit mantissa multiply by 10 ;-------------------------------- ulac = 0 ; unsigned long inout: ac = ((ac << 2) + ac) << 1; ulmq = ulac+4 ; unsigned long local ;-------------------------------- mul10: lda ulac sta ulmq ; ulmq = ulac; asl sta ulac ; ulac <<= 1; lda ulac+1 sta ulmq+1 rol sta ulac+1 lda ulac+2 sta ulmq+2 rol sta ulac+2 lda ulac+3 sta ulmq+3 rol sta ulac+3 asl ulac ; ulac <<= 1; rol ulac+1 rol ulac+2 rol ulac+3 clc ; ulac += ulmq; lda ulac adc ulmq sta ulac lda ulac+1 adc ulmq+1 sta ulac+1 lda ulac+2 adc ulmq+2 sta ulac+2 lda ulac+3 adc ulmq+3 sta ulac+3 asl ulac ; ulac <<= 1; rol ulac+1 rol ulac+2 rol ulac+3 rts

The 32bit input value is in accumulator AC, exactly memory locations AC to AC+3. This value is copied to register MQ, exactly memory locations MQ to MQ+3, and the AC value is shift left by one bit, that is multiply by two. Second step is shift left AC again. Now we have 4 times input value in AC and input value in MQ. Third step is add MQ to AC to get five times input value. Last step is shift left AC to get input value times 10.

Radix 10 to radix 2, negative exponent

To convert negative radix 10 exponent, the algorithm increases the radix 10 exponent by one and divides the mantissa by 10 to compensate. There is no while loop around the div10() operation, because one division by 10 needs several multiply by 2 to compensate.

The constant Max2 defines the maximum number that allows a multiply by 2 without overflow. The case if (e10 > 0) got changed to if (e10 >= 0). Details see below.

/* a2f2.c */ #include <stdio.h> #define Guard 8 #define Round 128 #define Max10H 0x1999 #define Max10L 0x9999 #define Max2H 0x7FFF #define Max2L 0xFFFF typedef union { unsigned long l; unsigned short s[2]; } UL; unsigned long asc2fp(e2_, m_, e10) /* out: radix 2 mantissa */ int *e2_; /* out: radix 2 exponent */ unsigned long m_; /* in: mantissa */ register int e10; /* in: radix 10 exponent */ { register UL m; register int e2 = 0; m.l = m_; printf(" %8luE%d\n", m.l, e10); if (0 == m.l) { *e2_ = 0; return 0; } m.l <<= Guard; printf(" %2d %8lu*2^%d 0x%08lx \n", e10, m.l>>8, e2, m); if (e10 >= 0) { for(;;) { while (m.s[1] < Max10H || (m.s[1] == Max10H && m.s[0] <= Max10L)) { m.l *= 10; --e10; printf("*10 %2d %8lu*2^%d 0x%08lx \n", e10, m.l>>8, e2, m); } if (e10 <= 0) break; while (m.s[1] > Max10H || (m.s[1] == Max10H && m.s[0] > Max10L)) { m.l /= 2; ++e2; printf("/2 %2d %8lu*2^%d 0x%08lx \n", e10, m.l>>8, e2, m); } } } if (e10 < 0) { for(;;) { while (m.s[1] < Max2H || (m.s[1] == Max2H && m.s[0] <= Max2L)) { m.l *= 2; --e2; printf("*2 %2d %8lu*2^%d 0x%08lx \n", e10, m.l>>8, e2, m); } if (e10 >= 0) break; m.l >>= 1; m.l /= 5; ++e10; printf("/10 %2d %8lu*2^%d 0x%08lx \n", e10, m.l>>8, e2, m); } } m.l >>= 1; /* avoid 0xfffffff0 problem */ m.l += 64; m.l >>= 7; *e2_ = e2; printf(" %8lu*2^%d\n", m.l, e2); return m.l; } int main() { static unsigned long m10[] = {9999999L, 9999999L, 100000L, 100000L}; static int e10[] = {-1, -2, 0, -1}; int i; for (i = 0; i < 4; ++i) { int e2; unsigned long m2 = asc2fp(&e2, m10[i], e10[i]); printf("\n"); } }

The first two test cases are simple. We see the known pattern of changing radix 10 exponent to 0 and changing radix 2 exponent from zero.

9999999E-1 -1 9999999*2^0 0x98967f00 /10 0 999999*2^0 0x0f423fe6 *2 0 1999999*2^-1 0x1e847fcc *2 0 3999999*2^-2 0x3d08ff98 *2 0 7999999*2^-3 0x7a11ff30 *2 0 15999998*2^-4 0xf423fe60 15999998*2^-4 9999999E-2 -2 9999999*2^0 0x98967f00 /10 -1 999999*2^0 0x0f423fe6 *2 -1 1999999*2^-1 0x1e847fcc *2 -1 3999999*2^-2 0x3d08ff98 *2 -1 7999999*2^-3 0x7a11ff30 *2 -1 15999998*2^-4 0xf423fe60 /10 0 1599999*2^-4 0x1869ffd6 *2 0 3199999*2^-5 0x30d3ffac *2 0 6399999*2^-6 0x61a7ff58 *2 0 12799998*2^-7 0xc34ffeb0 12799999*2^-7 The next two test cases have not-normalized mantissa. Our algorithm first normalizes this mantissa, before the "real" conversion starts. The algorithm can convert a mantissa value low as 1 to a normalized mantissa, too. Only mantissa value of 0 remains a special case.

100000E0 0 100000*2^0 0x0186a000 *10 -1 1000000*2^0 0x0f424000 *10 -2 10000000*2^0 0x98968000 /10 -1 1000000*2^0 0x0f424000 *2 -1 2000000*2^-1 0x1e848000 *2 -1 4000000*2^-2 0x3d090000 *2 -1 8000000*2^-3 0x7a120000 *2 -1 16000000*2^-4 0xf4240000 /10 0 1600000*2^-4 0x186a0000 *2 0 3200000*2^-5 0x30d40000 *2 0 6400000*2^-6 0x61a80000 *2 0 12800000*2^-7 0xc3500000 12800000*2^-7 100000E-1 -1 100000*2^0 0x0186a000 *2 -1 200000*2^-1 0x030d4000 *2 -1 400000*2^-2 0x061a8000 *2 -1 800000*2^-3 0x0c350000 *2 -1 1600000*2^-4 0x186a0000 *2 -1 3200000*2^-5 0x30d40000 *2 -1 6400000*2^-6 0x61a80000 *2 -1 12800000*2^-7 0xc3500000 /10 0 1280000*2^-7 0x13880000 *2 0 2560000*2^-8 0x27100000 *2 0 5120000*2^-9 0x4e200000 *2 0 10240000*2^-10 0x9c400000 10240000*2^-10

68000 assembler Radix 10 to radix 2, negative exponent

The 68000 CPU has 32bit registers. The 32bit mantissa occupies one 68000 register. The Z80 needs two register pairs for the mantissa and the 6502 needs four 8bit memory locations.

* a2f6.s .globl _asc2fp .text _asc2fp: link A6,#0 movem.l D4-D7,-(sp) move.l 12(A6),D7 * { D7 = m move.b 17(A6),D6 * D6 = e10 moveq #0,D5 * register char e2 = 0; move.l D7,D0 * if (0 == m) { bne.s endi1 move.l 8(A6),A0 * *e2_ = 0; clr.b (A0) moveq #0,D0 * return 0; bra.s retu1 endi1: * } lsl.l #8,D7 * m <<= Guard; move.b D6,D0 * if (e10 >= 0) { blt.s endi2 fore1: * for(;;) { bra.s tst1 * while (m <= Max10) { whle1: move.l D7,D0 * m = ((m << 2) + m) << 1; lsl.l #2,D7 add.l D0,D7 lsl.l #1,D7 sub.b #1,D6 * --e10; tst1: cmp.l #$19999999,D7 * } bls.s whle1 move.b D6,D0 * if (e10 <= 0) break; ble.s endi2 bra.s tst2 * while (m > Max10) { whle2: lsr.l #1,D7 * m >>= 1; add.b #1,D5 * ++e2; tst2: cmp.l #$19999999,D7 * } bhi.s whle2 bra.s fore1 * } endi2: * } move.b D6,D0 * if (e10 < 0) { bge.s endi3 fore2: * for(;;) { bra.s tst3 * while (m <= Max2) { whle3: add.l D7,D7 * m += m; sub.b #1,D5 * --e2; tst3: cmp.l #$7fffffff,D7 * } bls.s whle3 move.b D6,D0 * if (e10 >= 0) break; bge.s endi3 bsr.s div10 * m /= 10; add.b #1,D6 * ++e10; bra.s fore2 * } endi3: * } lsr.l #1,D7 * m >>= 1; add.l #$40,D7 * m += 64; lsr.l #7,D7 * m >>= 7; move.l 8(A6),A0 * *e2_ = e2; move.b D5,(A0) move.l D7,D0 * return m; retu1: tst.l (sp)+ movem.l (sp)+,D5-D7 unlk A6 rts * }

This is CP/M 68K AS68 assembler. On average, one C language source code line translates into two assembler code lines. This assembler code has input parameters and output result as needed by Alcyon C compiler. The input parameters are on stack, the output result is register D0.
The assembler code is based on the assembler output of the Alycon C compiler. The C compiler transcribes the conditional statements from C to assembler.

C language	Assembler	Jump	Name, use of flags	Type
`if (0 == m) {`	`move.l D7,D0` `bne.s endi1`	away	Branch Not Equal Branch if Z == 0	don't care
`if (e10 >= 0) {`	`move.b D6,D0` `blt.s endi2`	away	Branch Less Then Branch if N != V	signed
`if (e10 <= 0) break;`	`move.b D6,D0` `ble.s endi2`	to	Branch Less or Equal Branch if Z == 1 or N != V	signed
`if (e10 < 0) {`	`move.b D6,D0` `bge.s endi3`	away	Branch Greater or Equal Branch if N == V	signed
`if (e10 >= 0) break;`	`move.b D6,D0` `bge.s endi3`	to	Branch Greater or Equal Branch if N == V	signed
`while (m <= Max10) {`	`cmp.l #$19999999,D7` `bls.s whle1`	to	Branch Lower or Same Branch if C == 1 or Z == 1	unsigned
`while (m > Max10) {`	`cmp.l #$19999999,D7` `bhi.s whle2`	to	Branch HIgher Branch if C == 0 and Z == 0	unsigned
`while (m <= Max2) {`	`cmp.l #$7fffffff,D7` `bls.s whle3`	to	Branch Lower or Same Branch if C == 1 or Z == 1	unsigned
`if (carry) {`	`sub.l D2,D7` `bcc.s endi4`	away	Branch Carry Clear Branch if C == 0	unsigned

To transcribe a C language if statement, we need at least two assembler opcodes. One to set the CPU flags, another to do the conditional branch (jump). The 68000 MOVE opcode sets the CPU flags.
The CMP opcode performs a subtraction. The register values do not change, only the CPU flags change.
The 68000 CPU has 14 different conditional branches. The branches BMI, BPL, BGE, BGT, BLE and BLT are specific for signed integer, the branches BCC, BCS, BHI and BLS are for unsigned integer. The branches BEQ and BNE are don't care. The branch BRA is unconditional.
To find the correct branch opcode, two questions are important: Jump away or jump to? Unsigned or signed?
I wrote the Z80 assembler version of radix 10 to radix 2 conversion first. Please read these comments for more information.

* unsigned 32bit mantissa divide by 10.0 by multiply by 0.1 * inout: D7 * uses D0, D1, D2 div10: * { moveq #32,D0 * short i = 32; bra.s strt1 do1: * do { roxr.l #1,D1 * ulmq >>= 1; ulmq.msb = xflag; lsr.l #1,D7 * ulac >>= 1; strt1: move.b D7,D2 * xflag = carry = ulac.lsb; lsr.b #1,D2 bcc.s endi4 * if (carry) { add.l #$1999999A,D1 * ulmq += 0x19999999L; endi4: * } dbra D0,do1 * } while (--i >= -1); move.l D1,D7 * ulac = ulmq; rts * }

This mantissa div10 subroutine is cheating. It is a multiply by 0.1 algorithm. The multiplier 0x1999999A is a Q 0.32 number with the decimal value 0.1.

* unsigned 32bit mantissa divide by 10 * inout: D7 * uses D0, D1, D2 div10: * { moveq #28,D0 * short i = 28; moveq #0,D1 * unsigned long q = 0L; move.l #$A0000000,D2 * unsigned long d = 0xA0000000L; do1: * do { sub.l D2,D7 * xflag = carry = n < d; n -= d; bcc.s endi4 * if (carry) { add.l D2,D7 * n += d; endi4: * } eori.b #$10,ccr * xflag = !xflag; addx.l D1,D1 * q += q; q |= xflag; lsr.l #1,D2 * d >>= 1; dbra D0,do1 * } while (--i >= -1); move.l D1,D7 * return q; rts * }

That mantissa div10 subroutine is a restoring division. The divisor 0xA0000000 is a Q 4.28 number with the decimal value 10.0.

Z80 assembler Radix 10 to radix 2, negative exponent

The Alcyon Motorola 68000 C compiler produces nearly optimum assembler (machine code). The Hi-Tech Z80 C compiler has faulty 32bit compare and does not use the alternate register set of the Z80. Therefore I optimized the Z80 assembler output of the following C header file:

/* a2f6.h */ #define Guard 8 #define Round 128 #define Max10 0x19999999L #define Max2 0x7FFFFFFFL extern unsigned long asc2fp(char *, unsigned long, char);

And C source code file:

/* a2f6.c */ #include "a2f6.h" unsigned long asc2fp(e2_, m, e10) /* out: radix 2 mantissa */ char *e2_; /* out: radix 2 exponent */ register unsigned long m; /* in: mantissa */ char e10; /* in: radix 10 exponent */ { char e2 = 0; if (0 == m) { *e2_ = 0; return 0; } m <<= Guard; if (e10 >= 0) { for(;;) { while (m <= Max10) { m *= 10; --e10; } if (e10 <= 0) break; while (m > Max10) { m /= 2; ++e2; } } } if (e10 < 0) { for(;;) { while (m <= Max2) { /* Normalize */ m *= 2; --e2; } if (e10 >= 0) break; m /= 10; ++e10; } } m >>= 1; /* avoid 0xfffffff0 problem */ m += 64; m >>= 7; *e2_ = e2; return m; }

The assembler listing has 206 lines. Included are 40 comment lines from the header file and the C source code file. I discuss the assembler listing in parts. The complete assembler listing is in the Zip file. See section download above.

;a2f6.h: 8: extern unsigned long asc2fp(char *, unsigned long, char); ;A2F6.C: 4: unsigned long asc2fp(e2_, m, e10) ;A2F6.C: 5: char *e2_; ;A2F6.C: 6: register unsigned long m; ;A2F6.C: 7: register char e10; ;A2F6.C: 8: { psect text global _asc2fp _asc2fp: global ncsv, cret, indir call ncsv defw f2

The comment lines start with a ; character. The subroutine entry point is _asc2fp:. The underscore is added by the C compiler to every C function name. The call ncsv and defw f2 opcodes do the "make place for local variables" job. At the end of the assembler listing f2 is defined:

f2 equ -1

There is one byte defined for local variables. Important for argument passing and local variables is the "stack frame". The Hi-Tech C compiler uses register IX as "frame pointer" or "base pointer". The ncsv subroutine uses the defw value after the call opcode to set register IX. The stack frame is:

ix+12 char e10 ix+11 ix+10 ix+9 ix+8 unsigned long m ix+7 ix+6 char *e2_ ... ix-1 char e2

The stack frame entries between ix-1 and ix+6 are used for return address and C runtime housekeeping. The 32bit variable m occupies from ix+8 to ix+11. Location ix+8 is least significant byte. The 16bit pointer variable e2_ is from ix+6 to ix+7 with ix+6 least significant byte.

ld l,(ix+8) ; begin register unsigned long m; ld h,(ix+1+8) exx ld l,(ix+2+8) ld h,(ix+3+8) exx ; end register unsigned long m; ld c,(ix+12) ; register char e10;

The value of m is copied into Z80 registers H'L'HL. The H' register is the H register of the alternate register set. Opcode exx switches between the register sets. The expression H'L'HL says: register H' holds the most significant byte, register L the least significant byte.

;A2F6.C: 9: char e2 = 0; ld b,0

The char type of Hi-Tech C compiler is a signed 8bit value. The Hi-Tech C float type uses 7bit for exponent, therefore we have 1 spare bit. Not much, but it is always nice if one C source code line translates into one assembler line.

;A2F6.C: 10:     if (0 == m) {     ld a,l     or h     exx     or l     or h     exx     jr nz,endi1 The or opcode reduces four bytes into one byte. Any bit with value 1 in the four bytes will produce a final byte with a value different from zero.
Note: The C source code test is "equal zero", but the assembler code needs a "jump away", therefore a "jump not zero".

;A2F6.C: 11:         *e2_ = 0;     ld l,(ix+6)     ld h,(ix+1+6)     ld (hl),0
The address of e2_ is in the stack frame. The Z80 can only use registers as pointers - this is "RISC like". That the Z80 can store a constant at (HL) is "CISC like".

;A2F6.C: 12:         return 0;     ld de,0     ld l,e     ld h,d     jp ret1 ;A2F6.C: 13:     } endi1: The Hi-Soft C runtime expects an "unsigned long" return value in registers HLDE.

;A2F6.C: 14:     m <<= 8;     ld a,h     ld h,l     ld l,0     exx     ld h,l     ld l,a     exx The "shift left 8 bits" operation is done as "shift left 1 byte". The A register helps to transfer one byte from normal register set to alternate register set. The least significant byte gets value zero.

;A2F6.C: 15:     if (e10 >= 0) {     ld a,c     or a     jp m,endi2 The Z80 has eight different conditional jumps. The compare opcode performs a subtraction. If we exchange the operands of the compare, we get 16 possibilities: a - b with eight different jumps, b - a with eight different jumps. The ld opcode does not change the flags, but "or a" does. Please remember that we need "jump away" logic.

;A2F6.C: 16:         for (;;) { fore1:
The "forever" loop is only a label. Further down in the assembler listing is an unconditional jump to this label.

;A2F6.C: 17:             while (m <= 0x19999999L) {     jr tst1 whle1:
The while loop is coded in two parts. The first part is a jump to the compare part of the while loop which is located at the end of the while loop. This second part has a conditional jump back to label whle1. This is one of the little "compiler tricks".

;A2F6.C: 18:                 m *= 10;     ld e,l             ; m = ((m << 2) + m) << 1;     ld d,h     add hl,hl     exx     ld e,l     ld d,h     adc hl,hl     exx     add hl,hl     exx     adc hl,hl     exx     add hl,de     exx     adc hl,de     exx     add hl,hl     exx     adc hl,hl     exx This is Z80 assembler at it's best. First contents of variable m or registers H'L'HL is copied to D'E'DE. Then we do two times "add with yourself", that is multiply m by four. Next we add the copy of m in D'E'DE to "four times m" to get "five times m". Last we "add with yourself" again to get "ten times m" as final result.

;A2F6.C: 19:                 --e10;     dec c This is simple.

tst1:     ld a,99h           ; begin m <= 0x19999999L     sub l     ld a,99h     sbc a,h     exx     ld a,99h     sbc a,l     ld a,19h     sbc a,h     exx                 ; end m <= 0x19999999L     jr nc,whle1 ;A2F6.C: 20:             } This is the second part of while loop. A compare in assembler is a special subtraction: we don't need the result, we only need the flags like carry and zero. The 32bit constant compare value of 0x19999999 is subtracted in four 8bit steps. Next to H'L'HL that contains m, we only need register A. Exactly this 32bit compare the Hi-Soft C compiler can not do correctly. The Hi-Soft C compiler is correct for up to 31bit compare.
The pattern "load constant to accumulator, subtract register" is the alternate compare pattern.
Note: You get a carry (flag) for n1 - n2, if n2 is larger then n1.

;A2F6.C: 21:             if (e10 <= 0) break;     xor a     cp c     jp p,endi3 I use the alternate sequence of opcodes before a conditional jump. Normal sequence is load register A with variable, compare constant and jump conditionally. Rewrite the C statement as "if (0 >= e10)" and remember that break needs a "jump to" logic.

;A2F6.C: 22:             while (m > 0x19999999L) {     jr tst2 whle2: Another first part of a while loop.

;A2F6.C: 23:                 m /= 2;     exx     srl h     rr l     exx     rr h     rr l Divide by two for unsigned values needs a "logical shift right" as first opcode, not an "arithmetic shift right".
Note: you can replace shift left with add, but not shift right with subtract!

;A2F6.C: 24:                 ++e2;     inc b Easy.

tst2:     ld a,99h           ; begin m > 0x19999999L     sub l     ld a,99h     sbc a,h     exx     ld a,99h     sbc a,l     ld a,19h     sbc a,h     exx                 ; end m > 0x19999999L     jr c,whle2 ;A2F6.C: 25:             } Another second part of a while loop. We use the same alternate compare pattern, but the opposite conditional jump to get opposite compares (less or equal versus greater).

;A2F6.C: 26:         }     jr fore1 ;A2F6.C: 27:     } endi2: endi3: This is the second part of the "forever" loop. Label endi3 is the jump target for "break".

;A2F6.C: 28:     if (e10 < 0) {     ld a,c     or a     jp p,endi4 This is now a well known normal "jump away" case.

;A2F6.C: 29:         for (;;) { fore2:
Well known forever loop.

;A2F6.C: 30:             while (m <= 0x7FFFFFFFL) {     jr tst3 whle3: Well known first part of while loop.

;A2F6.C: 31:                 m *= 2;     add hl,hl     exx     adc hl,hl     exx The algorithm is m += m instead of m *= 2, the result is the same.

;A2F6.C: 32:                 --e2;     dec b Simple.

tst3:     exx                 ; begin m <= 0x7FFFFFFFL     ld a,h     exx     or a               ; end m <= 0x7FFFFFFFL     jp p,whle3 ;A2F6.C: 33:             } The value 0x7FFFFFFFL is the largest positive signed integer. Therefore I can use the most significant bit to simplify the compare.

;A2F6.C: 34:             if (e10 >= 0) break;     ld a,c     or a     jp p,endi5 Well known if implementation in assembler.

;A2F6.C: 35:             m /= 10;     push    bc     call    uldiv10     pop bc Because we use registers BC as register variables and subroutine uldiv uses registers BC as scratch registers, I save registers BC on stack. The uldiv10 subroutine could be inline.

;A2F6.C: 36:             ++e10;     inc c Simple.

;A2F6.C: 37:         }     jr fore2 ;A2F6.C: 38:     } endi4: endi5: This is second part of forever loop.

;A2F6.C: 39:     m += 128;     ld de,128     add hl,de     exx     ld de,0     adc hl,de Rounding is done as "add the value of 0.5 times least significant bit, then truncate".

;A2F6.C: 40:     m >>= 8;     ld a,l     ld l,h     ld h,0     exx     ld l,h     ld h,a The "shift right 8 bits" operation is done as "shift right 1 byte".

;A2F6.C: 41:     *e2_ = e2;     ld a,b     ld e,(ix+6)     ld d,(ix+1+6)     ld (de),a Normally registers HL are used as pointer. But H'L'HL contains still value of m. Registers DE are scratch or temporary registers.

;A2F6.C: 42:     return m;     ld e,l     ld d,h     exx     ld a,l     exx     ld l,a     exx     ld a,h     exx     adc a,0             ; avoid 0xFFFFFFF0 problem     ld h,a All ld opcodes do not change flags. The rounding adds can leave carry flag set. The "adc a,0" opcode brings this carry into the most significant byte. The Hi-Soft C runtime expects an "unsigned long" return value in registers HLDE.

;A2F6.C: 43: } ret1:     jp cret     f2 equ -1

This is more C runtime housekeeping. I assume "jump cret" cleans the stack frame before return from subroutine.
To transcribe "C compiler assembler output" to "optimized assembler output" was a manual multi step process. In the 1980s I wrote an optimized 32bit integer package for the Z80 for my employer. Maybe there is a Z80 C compiler that can produce "optimized assembler output" by itself. I doubt. But feel free to write your own optimized Z80 C compiler.

The "test driver" C program is:

/* ta2f6.c */ #include <stdio.h> #include "a2f6.h" int main() {     unsigned long m10, m2;     char e10, e2;     for (e10 = -4; e10 <= 4; ++e10) {         for (m10 = 0x199999L; m10 <= 0x19999AL; ++m10) {             m2 = asc2fp(&e2, m10, e10);             printf("%luE%-2d %8lu*2^%-3d 0x%06lx 0x%02x\n",                 m10, e10, m2, e2, m2, e2);         }     } } The Hi-Soft C compiler allows easy compiling, assembling and linking with one command:

c ta2f6.c a2f6.as The output is:

C>ta2f6 1677721E-4 10995112*2^-16 0xA7C5A8 0xFFF0 1677722E-4 10995119*2^-16 0xA7C5AF 0xFFF0 1677721E-3 13743890*2^-13 0xD1B712 0xFFF3 1677722E-3 13743899*2^-13 0xD1B71B 0xFFF3 1677721E-2 8589932*2^-9 0x83126C 0xFFF7 1677722E-2 8589937*2^-9 0x831271 0xFFF7 1677721E-1 10737414*2^-6 0xA3D706 0xFFFA 1677722E-1 10737421*2^-6 0xA3D70D 0xFFFA 1677721E0 13421768*2^-3 0xCCCCC8 0xFFFD 1677722E0   1677722*2^0   0x19999A 0x00 1677721E1 16777210*2^0   0xFFFFFA 0x00 1677722E1   8388610*2^1   0x800002 0x01 1677721E2 10485756*2^4   0x9FFFFC 0x04 1677722E2 10485763*2^4   0xA00003 0x04 1677721E3 13107195*2^7   0xC7FFFB 0x07 1677722E3 13107203*2^7   0xC80003 0x07 1677721E4 16383994*2^10 0xF9FFFA 0x0A 1677722E4 16384004*2^10 0xFA0004 0x0A
The radix 2 "normalized mantissa" has value from 0x800000 to 0xFFFFFF hexadecimal or 8388608 to 16777215 decimal. The book "The complete ZX81 ROM disassembly" by Ian Logan and Frank O'Hara contains Z80 assembly code for radix 10 to radix 2 conversion. This was my first contact with the topic. The ZX81 programmers goal was minimum size. Later I looked at radix conversion in Microsoft Basic for Intel 8080, originally written by Monte Davidoff. My implementation is hopefully more accurate, faster and easier to understand then the older implementations.´

6502 assembler Radix 10 to radix 2, negative exponent

Steve Wozniak and Roy Rankin published in August 1976 in Dr Dobb's journal "Floating point routines for the 6502". There were no radix conversion subroutines in this package. The a2f6.c source code can be transcribed to 6502 assembler.

; a2f6.65s ; radix 10 to radix 2 conversion ;-------------------------------- expo = 0 ; out: radix 2 exponent, signed 8bit mani = expo+1 ; inout: mantissa, unsigned 32bit mano = mani+4 ; local: mantissa, unsigned 32bit expi = mano+4 ; in: radix 10 exponent, signed 8bit ;-------------------------------- asc2fp: ; void asc2fp() ; { jsr prhex stz expo ; expo = 0; lda mani ; if (0 == m) { ora mani+1 ora mani+2 ora mani+3 bne .endi1 stz expo ; expo = 0; stz mani ; m = 0; stz mani+1 stz mani+2 stz mani+3 rts ; return; .endi1: ; } lda mani+2 ; m <<= Guard; sta mani+3 lda mani+1 sta mani+2 lda mani sta mani+1 stz mani

This is 65C02 assembler code, because I have a 65C02 CPU. I bought it in 2022 from Mouser. It was new, not new old stock (NOS). I use the STZ and BRA opcodes. Backport to 6502 assembler is easy.
The 6502 subroutine uses "well known" memory addresses for argument input and result output. This is FORTRAN (no recursive programming) style argument passing. Argument passing on stack is no good idea for 6502. The 6502 CPU has 3500 transistor functions, the Z80 has 8200 and the Motorola 68000 has 68000. Only 256 bytes stack memory and only three 8-bits registers are 6502 limitations. Still, the 6502 is a nice CPU and fun to program.
The subroutine prhex emits logging information for debugging. The 6502 Macroassembler & simulator has a "simulator console" to show this logging information. Very handy!
The assembler code comment is the C language source code.

lda expi ; if (expi >= 0) { bmi .endi2 .fore1: ; for (;;) { bra .tst1 ; while (m <= Max10) { .whle1: jsr mul10 ; m = mul10(m); dec expi ; --expi; jsr prhex .tst1: sec lda #$99 sbc mani lda #$99 sbc mani+1 lda #$99 sbc mani+2 lda #$19 sbc mani+3 bcs .whle1 ; } lda #0 ; if (expi <= 0) break; cmp expi bpl .endi2 bra .tst2 ; while (m > Max10) { .whle2: lsr mani+3 ; m >>= 1; ror mani+2 ror mani+1 ror mani inc expo ; ++expo; jsr prhex .tst2: sec lda #$99 sbc mani lda #$99 sbc mani+1 lda #$99 sbc mani+2 lda #$19 sbc mani+3 bcc .whle2 ; } bra .fore1 ; } .endi2: ; }

The program logic is as in the Z80 assembler code. The 6502 has a speciality with the SBC opcode: You have to use SEC (set carry flag) before SBC. And the carry flag result of SBC is opposite to the Z80 SBC carry flag result.
Another difference: the 6502 load opcodes change the zero and negative flags, the Z80 load opcodes change no flags.
The mul10 subroutine is presented above. Some additional opcode copy the mul10 output from MQ memory locations to AC memory locations. Memory location mani (mantissa in) is an alias to AC, mano (mantissa out) is an alias to MQ.

lda expi ; if (expi < 0) { bpl .endi3 .fore2: ; for (;;) { bra .tst3 ; while (m <= Max2) { .whle3: asl mani ; m <<= 1; rol mani+1 rol mani+2 rol mani+3 dec expo ; --expo; jsr prhex .tst3: lda mani+3 bpl .whle3 ; } lda expi ; if (expi >= 0) break; bpl .endi3 jsr div10 ; m = div10(m); lda ulmq ; ulac = ulmq; sta ulac lda ulmq+1 sta ulac+1 lda ulmq+2 sta ulac+2 lda ulmq+3 sta ulac+3 inc expi ; ++expi; jsr prhex bra .fore2 ; } .endi3: ; }

The processing of negative radix 10 exponent is nice, tight code. The subroutine div10 is presented above.

clc ; m += 128; m >>= Guard; lda mani adc #128 lda mani+1 adc #0 sta mani lda mani+2 adc #0 sta mani+1 lda mani+3 adc #0 sta mani+2 lda #0 adc #0 sta mani+3 jsr prhex rts ; }

The maximum mantissa output value is 0x1000000, because rounding can "ripple through" to the most significant bit. The "doing 8-bit at a time" approach of the 6502 has advantages.

6502 Simulator logging window. First column is mantissa in hexadecimal, second column is radix 2 exponent. The radix 10 decimal input value is 1677721E-1, the radix 2 decimal output value is 10737414*2^-6.
The 6502 code density is poor compared to Z80 and 68000. Most 6502 opcode of the a2f6 program assemble to 2 bytes. A lot of Z80 a2f6 program opcodes assemble to 1 byte. The 6502 performs better on "lines of code". No EXX opcodes needed for alternate registers or OR A opcodes for set flags.
6502 code size for subroutines div10, mul10 and asc2fp is 309 bytes decimal. Z80 code size for div10 and asc2fp is 229 bytes decimal. 68000 code size for div10 and asc2fp is 126 bytes decimal.

Mantissa sign bit

Up to now, the mantissa sign bit was not important. The algorithm uses signed magnitude, that is the mantissa is always positive and the sign is "it's own thing". A floating point number of this kind has three components: mantissa sign, mantissa value and two's complement exponent.

Floating point number interpretation

The interpretation of the input of asc2fp() function is: "positive integer mantissa, two's complement exponent". Up to now, we use the same interpretation for asc2fp() output. But arithmetic becomes easier if the mantissa is defined as normalized fraction of range 0.5 to 0.999... As integer mantissa, the binary point is right of the mantissa. As (true) fraction, the binary point is left of the mantissa. To shift the binary point, we just have to move the binary point 24 bits left by adding 24 to the exponent.
The IEEE754 floating point standard defines the mantissa as Q 1.23 unsigned fixed point number, that is one bit before the binary point and 23 bits after. For this interpretation, we add 23 to the exponent.
The battle plan for conversion and calculation should now be obvious:
1) Scan radix 10 ASCII string input
2) convert from radix 10 to radix 2 with integer mantissa
3) change radix 2 integer mantissa to fixed point mantissa
4) do radix 2 calculations like floating point add, sub, mul, div, ...
5) change radix 2 fixed point mantissa to integer mantissa
6) convert from radix 2 to radix 10 with integer mantissa
7) Print radix 10 ASCII string output

The traditional FP conversion is tricky, isn't it? It is a "transforming pipeline" of different representation of the same information. The pipeline is "slightly lossy" by maximum one mantissa bit due to limited accuracy in the process.

Pack/unpack floating point to IEEE754 format

The 32bit IEEE754 floating point format is today the most important "packaging" for floating point numbers. The C language definition of this package is FP. The function fp2float() packs from radix 2 to IEEE754. The function float2fp() unpacks. First, we write the numbers 0.9999999, 1.0 as integer mantissa radix 10: 9999999*10^-7, 10000000*10^-7. Second we run the test program:

/* a2f3.c */ /* IEEE754 32-bit floating point */ #include <stdlib.h> typedef struct { unsigned long m: 23; unsigned long e: 8; unsigned long s: 1; } FP; typedef union { float f; unsigned long l; FP x; } FL; float fp2float(sign, man, exp) /* out: IEEE754 fp */ register int sign; /* in: sign */ register unsigned long man; /* in: radix 2 mantissa */ register int exp; /* in: radix 2 exponent */ { register FL fp; exp += 127 + 23; if (exp < 1) { exp = 1; man = 0; } else if (exp >= 254) { exp = 254; man = 0xFFFFFFL; } fp.x.m = man; /* truncate leading bit */ fp.x.e = exp; fp.x.s = sign; /* printf(" fp2float 0x%08lx\n", fp.l); */ return fp.f; } unsigned long float2fp(sign, exp, f) /* out: radix 2 mantissa */ int *sign; /* out: sign */ int *exp; /* out: radix 2 exponent */ register float f; /* in: IEEE754 fp */ { register FL fp; fp.f = f; if (0 == fp.l) { /* special case zero */ *sign = 0; *exp = 0; return 0L; } *sign = fp.x.s; *exp = fp.x.e - 127 - 23; /* printf(" float2fp 0x%08lx\n", fp.l); */ return fp.x.m + 0x800000L; /* add leading bit */ } int main() { static unsigned long m10[] = {9999999L, 10000000L, 5400000L, 9200000L}; static int e10[] = {-7, -7, -26, 12}; int i; for (i = 0; i < 4; ++i) { unsigned long m2i, m2o; int e2i, e2o, sign; float f; printf("%lu*10^%d\n", m10[i], e10[i]); m2i = asc2fp(&e2i, m10[i], e10[i]); f = fp2float(0, m2i, e2i); printf("%lu*2^%d = %e\n", m2i, e2i, f); m2o = float2fp(&sign, &e2o, f); printf("%e = %lu*2^%d\n", f, m2o, e2o); printf("\n"); } }
Note: We need functions div10() and asc2fp() from the source code above. I commented the printf() statements in these functions to reduce output. Feel free to enable the full trace.

Output is:

9999999*10^-7 16777214*2^-24 = 9.999999e-01 9.999999e-01 = 16777214*2^-24 10000000*10^-7 8388608*2^-23 = 1.000000e+00 1.000000e+00 = 8388608*2^-23 5400000*10^-26 16712190*2^-88 = 5.400000e-20 5.400000e-20 = 16712190*2^-88 9200000*10^12 16734702*2^39 = 9.200000e+18 9.200000e+18 = 16734702*2^39 We use the C library function printf() for IEEE754 floating point format to radix 10 conversion. Everything looks right.

Pack/unpack floating point to Motorola MC68343 format

The Motorola MC68343 was not a hardware chip, but the name of the "Fast Floating Point" (FFP) assembler library for the Motorola 68000 CPU. It is a 32bit floating point "packaging". The CP/M 68K Alcyon C compiler uses FFP. There are differences in the definition of FP and the functions fp2float() and float2fp():

/* a2f3.c */ /* MC68343 32bit floating point */ float atof(); typedef struct { unsigned long e: 7; unsigned long s: 1; unsigned long m: 24; } FP; typedef union { float f; unsigned long l; FP x; } FL; float fp2float(sign, man, exp) /* out: MC68343 fp */ register int sign; /* in: sign */ register unsigned long man; /* in: radix 2 mantissa */ register int exp; /* in: radix 2 exponent */ { register FL fp; exp += 65 + 23; if (exp < 0) { exp = 0; man = 0; } else if (exp >= 127) { exp = 127; man = 0xFFFFFFL; } fp.x.m = man; fp.x.e = exp; fp.x.s = sign; /* printf(" fp2float 0x%08lx\n", fp.l); */ return fp.f; } unsigned long float2fp(sign, exp, f) /* out: radix 2 mantissa */ int *sign; /* out: sign */ int *exp; /* out: radix 2 exponent */ register float f; /* in: MC68343 fp */ { register FL fp; fp.f = f; if (0 == fp.l) { /* special case zero */ *sign = 0; *exp = 0; return 0L; } *sign = fp.x.s; *exp = fp.x.e - 65 - 23; /* printf(" float2fp 0x%08lx\n", fp.l); */ return fp.x.m; } The test program main() is as above.
The FFP format uses 24bits for mantissa, IEEE754 only 23. IEEE754 uses "hidden leading bit": The most significant bit of a normalized mantissa is always 1. FFP has this constant bit in the packaging, IEEE754 has not. Because for FFP the mantissa is larger, the exponent is smaller. The 7bits exponent uses bias 65 coding, not two's complement. The IEEE754 uses bias 127 coding. Last but not least the order of the components is different. IEEE754 has the order sign, exponent, mantissa and FFP has the order mantissa, sign, exponent.
Compile the source code file a2f3.c on a CP/M 68K machine like 68k-MBC with:

c a2f3 clinkf a2f3
Output is:

C>a2f3 9999999*10^-7 16777214*2^-24 = 9.999999E-01 9.999999E-01 = 16777214*2^-24 10000000*10^-7 8388608*2^-23 = 1.000000E00 1.000000E00 = 8388608*2^-23 5400000*10^-26 16712190*2^-88 = -0.000000E00 -0.000000E00 = 16712190*2^-88 9200000*10^12 16734702*2^39 = 9.223371E18 9.223371E18 = 16777215*2^39

Pack/unpack floating point to Hi-Tech C Z80 format

The Z80 floating point format is 1 mantissa sign bit, 7 exponent bits and 24 mantissa bits. The Hi-Tech C compiler can only handle 16bit unsigned int bitfields.

/* a2f3.c */ /* CP/M Hi-Tech C Z80 32bit floating point */ #include <math.h> typedef struct { unsigned int ml: 16; /* Hi-Tech C has only unsigned int bitfield */ unsigned int mh: 8; unsigned int e: 7; unsigned int s: 1; } FP; typedef union { float f; unsigned long l; FP x; } FL; float fp2float(sign, man, exp) /* out: Hi-Tech C Z80 fp */ register int sign; /* in: sign */ register unsigned long man; /* in: radix 2 mantissa */ register int exp; /* in: radix 2 exponent */ { register FL fp; exp += 65 + 23; if (exp < 0) { exp = 0; man = 0; } else if (exp >= 127) { exp = 127; man = 0xFFFFFFL; } fp.l = man; /* hack */ fp.x.e = exp; fp.x.s = sign; /* printf(" fp2float 0x%08lx\n", fp.l); */ return fp.f; } unsigned long float2fp(sign, exp, f) /* out: radix 2 mantissa */ int *sign; /* out: sign */ int *exp; /* out: radix 2 exponent */ register float f; /* in: Hi-Tech C Z80 fp */ { register FL fp; fp.f = f; if (0 == fp.l) { /* special case zero */ *sign = 0; *exp = 0; return 0L; } *sign = fp.x.s; *exp = fp.x.e - 65 - 23; /* printf(" float2fp 0x%08lx\n", fp.l); */ return fp.l & 0xFFFFFFL; /* hack */ }
Note: the "hack" avoids combining the mantissa out of low and high parts.
Compile the program with:

c a2f3.c -LF

The output is:

Radix 2 to radix 10

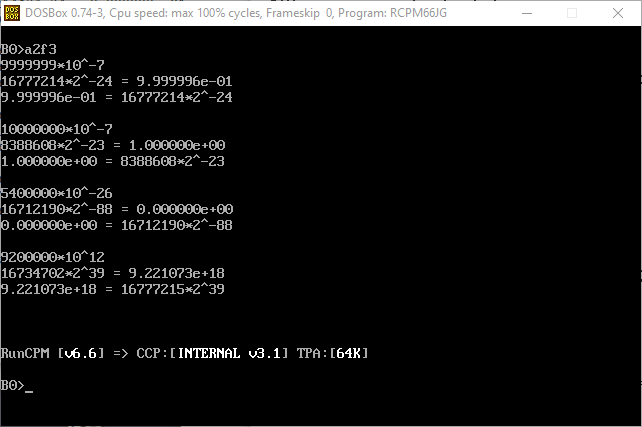
Radix 2 to radix 10 conversion is like radix 10 to radix 2 conversion. In the e2 < 0 part is a special case. We have to check that e2 does not become positive. Not handling this special case produced eErr messages in the test program. It is good to test the "impossible cases", too. If you make an error in design, it is natural to repeat this error in coding.

unsigned long fp2asc(e10_, m, e2) /* out: radix 10 mantissa */ int *e10_; /* out: radix 10 exponent */ register unsigned long m; /* in: radix 2 mantissa */ register int e2; /* in: radix 2 exponent */ { register int e10 = 0; if (0 == m) { *e10_ = 0; return 0; } m <<= Guard; if (e2 >= 0) { for (;;) { while (m <= Max2) { m += m; --e2; } if (e2 <= 0) break; m = div10(m); ++e10; } } if (e2 < 0) { for (;;) { while (m <= Max10) { /* Normalize */ m = ((m << 2) + m) << 1; --e10; } if (e2 >= 0) break; while (m > Max10 && e2 < 0) { m >>= 1; ++e2; } } } m >>= 1; /* avoid 0xfffffff0 problem */ m += 64; m >>= 7; *e10_ = e10; return m; } #define MA 0x19999AL #define MZ 0xFFFE12L void func(a, z) int a, z; { int e10i; for (e10i = a; e10i <= z; ++e10i) { int eErr = 0; int hits[9]; unsigned long m10i; int i; for (i = 0; i < 9; ++i) hits[i] = 0; for (m10i = MA; m10i < MZ; m10i += 15099L) { unsigned long m2o, m10o; int e2o, e10o; m2o = asc2fp(&e2o, m10i, e10i); m10o = fp2asc(&e10o, m2o, e2o); if (e10i != e10o) { ++eErr; printf("eErr %lue%d != %lue%d\n", m10i, e10i, m10o, e10o); } else { long ndx = 4+m10o-m10i; if (ndx < 0) ndx = 0; if (ndx > 8) ndx = 8; ++hits[ndx]; } } printf("%3d %2d", e10i, eErr); for (i = 0; i < 9; ++i) { if (i != 4) { printf(" %6d", hits[i]); } } printf("\n"); } } int main() { printf("10^ eErr <=-4 -3 -2 -1 1 2 3 >=4\n"); func(-18, -14); func(-2, 2); func(14, 18); } Every row of output of the test program is the result of converting 1000 numbers from radix 10 to radix 2 and back to radix 10. Column "10^" tells the radix 10 exponent, column "eErr" counts the radix 10 exponent mismatches. The following columns "<=-4" to ">=4" show the differences between radix 10 mantissa value going in and radix 10 mantissa value going out. Only the columns -2, -1 and 1 have values larger zero. This shows our "slightly lossy" transformation pipeline in action.

The output of all compilers is:

C>a2f4 10^ eErr <=-4 -3 -2 -1 1 2 3 >=4 -18 0 0 0 3 306 0 0 0 0 -17 0 0 0 0 287 0 0 0 0 -16 0 0 0 0 248 0 0 0 0 -15 0 0 0 1 234 0 0 0 0 -14 0 0 0 0 207 0 0 0 0 -2 0 0 0 0 39 49 0 0 0 -1 0 0 0 0 0 83 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 28 56 0 0 0 2 0 0 0 0 37 50 0 0 0 14 0 0 0 0 207 0 0 0 0 15 0 0 0 0 232 0 0 0 0 16 0 0 0 1 263 0 0 0 0 17 0 0 0 0 285 0 0 0 0 18 0 0 0 0 306 0 0 0 0

Note: The 68008 solution uses C with register variables. The Z80 solution uses optimized assembler for functions asc2fp() and fp2asc(). Execution time for Z80 on Z80-MBC2 computer with 8MHz clock is 2:07 minutes, for 68008 on 68k-MBC computer with 8MHz clock is 1:41 minutes. The limiting factors are the 8bit wide data bus and 8MHz clock speed for both computers.

Z80 assembler Radix 2 to radix 10

The Hi-Tech Z80 C compiler has faulty 32bit compare and does not use the alternate register set of the Z80. Therefore I optimized the Z80 assembler output of the following C header file:

/* a2f7.h */ #define Guard 8 #define Round 128 #define Max10 0x19999999L #define Max2 0x7FFFFFFFL extern unsigned long fp2asc(char *, unsigned long, char);

And C source code file:

/* a2f7.c */ #include "a2f7.h" unsigned long fp2asc(e10_, m, e2) /* out: radix 10 mantissa */ char *e10_; /* out: radix 10 exponent */ register unsigned long m; /* in: radix 2 mantissa */ register char e2; /* in: radix 2 exponent */ { register char e10 = 0; if (0 == m) { *e10_ = 0; return 0; } m <<= Guard; if (e2 >= 0) { for (;;) { while (m <= Max2) { m *= 2; --e2; } if (e2 <= 0) break; m /= 10; ++e10; } } if (e2 < 0) { for (;;) { while (m <= Max10) { /* Normalize */ m *= 10; --e10; } if (e2 >= 0) break; while (e2 < 0 && m > Max10) { m /= 2; ++e2; } } } m >>= 1; /* avoid 0xfffffff0 problem */ m += 64; m >>= 7; *e10_ = e10; return m; }

The assembler listing has 212 lines. The complete assembler listing is in the Zip file.
The "test driver" C program is:

/* ta2f7.c */ #include <stdio.h> #include "a2f7.h" int main() { unsigned long m2; char e2; for (e2 = -12; e2 <= 12; e2 += 3) { for (m2 = 0x199999L; m2 <= 0x19999AL; ++m2) { unsigned long m10; char e10; m10 = fp2asc(&e10, m2, e2); printf("%lu*2^%-3d %8luE%-2d 0x%06lx 0x%02x\n", m2, e2, m10, e10, m10, e10); } } } The Hi-Soft C compiler allows easy compiling, assembling and linking with one command:

c ta2f7.c a2f7.as The output is:

C>ta2f7 1677721*2^-12 4095999E-4 0x3E7FFF 0xFFFC 1677722*2^-12 4096001E-4 0x3E8001 0xFFFC 1677721*2^-9 3276799E-3 0x31FFFF 0xFFFD 1677722*2^-9 3276801E-3 0x320001 0xFFFD 1677721*2^-6 2621439E-2 0x27FFFF 0xFFFE 1677722*2^-6 2621441E-2 0x280001 0xFFFE 1677721*2^-3 2097151E-1 0x1FFFFF 0xFFFF 1677722*2^-3 2097153E-1 0x200001 0xFFFF 1677721*2^0 16777210E-1 0xFFFFFA 0xFFFF 1677722*2^0 1677722E0 0x19999A 0x00 1677721*2^3 13421768E0 0xCCCCC8 0x00 1677722*2^3 13421776E0 0xCCCCD0 0x00 1677721*2^6 10737414E1 0xA3D706 0x01 1677722*2^6 10737421E1 0xA3D70D 0x01 1677721*2^9 8589932E2 0x83126C 0x02 1677722*2^9 8589937E2 0x831271 0x02 1677721*2^12 6871945E3 0x68DB89 0x03 1677722*2^12 6871949E3 0x68DB8D 0x03
The radix 10 "normalized mantissa" has value from 0x19999A to 0xFFFFFF hexadecimal or 1677722 to 16777215 decimal.

Floating point conversion accuracy

The program a2f5.c shows the accuracy of the floating point library that you get with the C compiler and the accuracy of my implementation of radix conversion. The functions asc2fp() and fp2asc() are the same as above. The functions fp2float() and float2fp() are specific for Z80 32bit float, 68000 FFP 32bit float and 80386 32bit IEEE754 float.

/* a2f5.c */ void func(a, z) int a, z; { int e10i; for (e10i = a; e10i <= z; ++e10i) { static char s[16]; unsigned long m10i = 10000000L, m2o, m2u, m10o; int e2o, e2u, e10o, sign; float f; sprintf(s, "%lue%d ", m10i, e10i); f = atof(s); m2o = asc2fp(&e2o, m10i, e10i); f = fp2float(0, m2o, e2o); m2u = float2fp(&sign, &e2u, f); m10o = fp2asc(&e10o, m2u, e2u); printf("%-13s atof=%13.6e a2f=%luE%d \n", s, f, m10o, e10o); } } int main() { func(-27, -20); func(7, 14); }

The Hi-Tech Z80 output is:

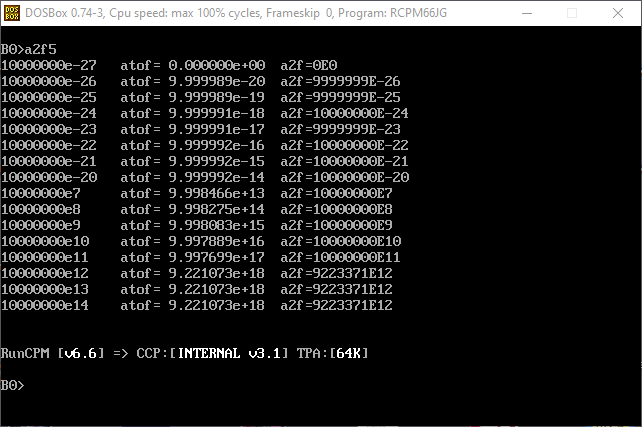
We can use the exponent range from 1e-19 to 1e18. Smaller and larger exponents can be used with asc2fp() and fp2asc(), but not with fp2float() and float2fp(). The "atof" column shows the low quality of the compiler library functions like atof() or printf() for floats.

The Alcyon 68000 output is:

C>a2f5 10000000e-27 atof= 0.000000E00 a2f=0E0 10000000e-26 atof= 1.000000E-19 a2f=9999999E-26 10000000e-25 atof= 1.000000E-18 a2f=9999999E-25 10000000e-24 atof= 1.000000E-17 a2f=10000000E-24 10000000e-23 atof= 1.000000E-16 a2f=9999999E-23 10000000e-22 atof= 1.000000E-15 a2f=10000000E-22 10000000e-21 atof= 1.000000E-14 a2f=10000000E-21 10000000e-20 atof= 1.000000E-13 a2f=10000000E-20 10000000e7 atof= 1.000000E14 a2f=10000000E7 10000000e8 atof= 1.000000E15 a2f=10000000E8 10000000e9 atof= 1.000000E16 a2f=10000000E9 10000000e10 atof= 1.000000E17 a2f=10000000E10 10000000e11 atof= 1.000000E18 a2f=10000000E11 10000000e12 atof= 9.223371E18 a2f=9223371E12 10000000e13 atof= 9.223371E18 a2f=9223371E12 10000000e14 atof= 9.223371E18 a2f=9223371E12

The Alcyon C library conversion is perfect. The function fp2float() has special cases underflow and overflow and limits the float value to minimum and maximum.

The gcc 80386 output is:

10000000e-27 atof= 1.000000e-20 a2f=9999999E-27 10000000e-26 atof= 1.000000e-19 a2f=9999999E-26 10000000e-25 atof= 9.999999e-19 a2f=9999999E-25 10000000e-24 atof= 1.000000e-17 a2f=10000000E-24 10000000e-23 atof= 1.000000e-16 a2f=9999999E-23 10000000e-22 atof= 1.000000e-15 a2f=10000000E-22 10000000e-21 atof= 1.000000e-14 a2f=10000000E-21 10000000e-20 atof= 1.000000e-13 a2f=10000000E-20 10000000e7 atof= 1.000000e+14 a2f=10000000E7 10000000e8 atof= 1.000000e+15 a2f=10000000E8 10000000e9 atof= 1.000000e+16 a2f=10000000E9 10000000e10 atof= 1.000000e+17 a2f=10000000E10 10000000e11 atof= 1.000000e+18 a2f=10000000E11 10000000e12 atof= 1.000000e+19 a2f=10000000E12 10000000e13 atof= 1.000000e+20 a2f=10000000E13 10000000e14 atof= 1.000000e+21 a2f=10000000E14

The exponent range of IEEE754 is larger, because it uses hidden leading mantissa bit. The gcc conversion works very well, but is not perfect.
The atof column numbers are different between the C compilers, but the a2f column numbers are the same. Some workarounds were needed for this success. The strength of C is to allow such workarounds.

Floating point addition

Floating point addition is easy. Just add two mantissas. Yes, but my C language floating point add function has nine if() and one while() to do the job. I hope, my solution has minimum complexity, good test-ability and is a complete solution.

/* tfadd.c */ float fadd(a, b) register double a, b; { int as, bs; int ae, be; register long am = float2fp(&as, &ae, a); register long bm = float2fp(&bs, &be, b); register int dexp = ae - be; if (dexp >= 24) { /* 1 */ return a; } if (dexp >= 1) { /* 2 */ bm >>= dexp; } dexp = 0 - dexp; if (dexp >= 24) { /* 3 */ return b; } if (dexp >= 1) { /* 4 */ am >>= dexp; ae = be; } if (as) { /* 5 */ am = 0 - am; } if (bs) { /* 6 */ bm = 0 - bm; } am += bm; if (0 == am) { /* 7 */ return 0.0; } as = 0; if (am < 0) { /* 8 */ as = 1; am = 0 - am; } if (am >= 0x1000000) { /* 9 */ am >>= 1; ++ae; } while (am < 0x800000) { am <<= 1; --ae; } return fp2float(as, am, ae); }

The maximum nesting level is 1. You can't do better. The test cases are my guideline to the source code. The test-driver is:

float af[] = {16777216.0, 8388608.0, -1.0, -1.0, 1.5, -1.5, 1.5, -1.5, 1.0, 1.0, 8388608.0}; float bf[] = { 1.0, 1.0, -16777216.0, -8388608.0, 0.5, 0.5, -0.5, -0.5, -1.0, 1.0, -8388607.0}; int main() { static char as[16], bs[16], cs[16]; int i; for (i=0; i < 11; ++i) { FL a, b, c; a.f = af[i]; b.f = bf[i]; c.f = fadd(a.f, b.f); printf("0x%08lx = 0x%08lx + 0x%08lx\n", c.l, a.l, b.l); printf("%12.1f = %12.1f + %12.1f\n", c.f, a.f, b.f); float2asc(as, a.f); float2asc(bs, b.f); float2asc(cs, c.f); printf("%12s = %12s + %12s\n", cs, as, bs); } }

There are 11 test cases. First test case matches first if().

0x4b800000 = 0x4b800000 + 0x3f800000 16777216.0 = 16777216.0 + 1.0 16777216e0 = 16777216e0 + 10000000e-7

First row is floating points as hexadecimal. Second row is gcc C compiler runtime representation. Third row is my radix 2 to radix 10 conversion. The difference of exponents is larger then 23, there are not enough mantissa bits for an addition. The larger number is returned. Second test case matches second if().

0x4b000001 = 0x4b000000 + 0x3f800000 8388609.0 = 8388608.0 + 1.0 8388609e0 = 8388608e0 + 10000000e-7

The result is different to the larger input number. The smaller input number was shifted to have the same exponent as the larger input number. Test cases three and four match if() three and four.

0xcb800000 = 0xbf800000 + 0xcb800000 -16777216.0 = -1.0 + -16777216.0 -16777216e0 = -10000000e-7 + -16777216e0 0xcb000001 = 0xbf800000 + 0xcb000000 -8388609.0 = -1.0 + -8388608.0 -8388609e0 = -10000000e-7 + -8388608e0

Same basic idea as test cases one and two, but this time for second argument. Test cases 5 to 8 test if() 5, 6 and 8.

0x40000000 = 0x3fc00000 + 0x3f000000 2.0 = 1.5 + 0.5 2000000e-6 = 15000000e-7 + 5000000e-7 0xbf800000 = 0xbfc00000 + 0x3f000000 -1.0 = -1.5 + 0.5 -10000000e-7 = -15000000e-7 + 5000000e-7 0x3f800000 = 0x3fc00000 + 0xbf000000 1.0 = 1.5 + -0.5 10000000e-7 = 15000000e-7 + -5000000e-7 0xc0000000 = 0xbfc00000 + 0xbf000000 -2.0 = -1.5 + -0.5 -2000000e-6 = -15000000e-7 + -5000000e-7

The arguments and the result can be positive or negative. For easy mantissa addition, I transform (unsigned) mantissa and mantissa-sign into a two's complement (signed) mantissa. The result is converted back to (unsigned) mantissa and mantissa-sign. The unsigned mantissa has 24bits. The sign bit needs one additional bit. The result of 0xFFFFFF + 0xFFFFFF is 0x1FFFFFE. Another additional bit is needed for adding large input numbers. For 24bit add we need at least 26bit accumulator. A 32bit accumulator is typical. Test case 9 tests if() 7.

0x00000000 = 0x3f800000 + 0xbf800000 0.0 = 1.0 + -1.0 0e0 = 10000000e-7 + -10000000e-7

A zero mantissa result is a special case for the following while() loop. Return float zero in this case. Test case 10 tests if() 9.

0x40000000 = 0x3f800000 + 0x3f800000 2.0 = 1.0 + 1.0 2000000e-6 = 10000000e-7 + 10000000e-7

This is normalizing a too big mantissa. Last test case tests while().

0x3f800000 = 0x4b000000 + 0xcafffffe 1.0 = 8388608.0 + -8388607.0 10000000e-7 = 8388608e0 + -8388607e0

This is mantissa bit canceling. The subtraction cancels all the leading mantissa bits to zero. Only the least significant bit is 1. This bit gets normalized.

Z80 floating point addition

The core of floating point addition, the mantissa addition, are tiny four lines of assembler starting at label endif6. The rest of 200 lines of assembler is mantissa alignment, exponent handling, sign handling and overflow/underflow processing.

;FADD.C: 3: float fadd(a, b) ;FADD.C: 4: register double a, b; ;FADD.C: 5: { psect text global _fadd, fadd2, fadd _fadd: global ncsv, cret, indir call ncsv defw f1 ;FADD.C: 6: return a + b; fadd2: ld e,(ix+10) ld d,(ix+1+10) ld l,(ix+6) ld h,(ix+1+6) exx ld e,(ix+2+10) ld d,(ix+3+10) ld l,(ix+2+6) ld h,(ix+3+6) exx

The first step is loading from stack frame to registers. The first argument is in stack frame locations ix+6 to ix+9, the second argument is in stack frame locations ix+10 to ix+13. The highest argument stack frame address contains the mantissa sign in bit 7 and the 7bit biased exponent.

;================================================== ; float addition routine ; hlde = h'l'hl + d'e'de ; needs registers a, b, c, b', c', changes flags ; fadd: exx ld a,d ; long bm = float2fp(&bs, &be, b); and 07Fh ; remove sign sub 65 ; remove bias ld c,a ; copy signed exp 2 ld a,h ; long am = float2fp(&as, &ae, a); and 07Fh ; remove sign sub 65 ; remove bias sub c ; dexp = ae - be; ld b,h ; copy sgn+exp 1 (as+ae) ld c,d ; copy sgn+exp 2 (bs+be) exx

Both exponent values are converted from biased value to two's complement number. The difference of exponent is calculated and stored in register A. The sgn+exp bytes of argument 1 and argument 2 are saved in registers B' and C'.

jp m,endif2 cp 24 ; if (dexp >= 24) { /* 1 */ jp nc,endfn1 ; return a; ; }

If dexp is negative, execution continues at label endif2. If argument 1 is much larger then argument 2, argument 1 is returned as result.

exx ld h,0 ; h'l'hl = am as 32bit mantissa ld d,h ; d'e'de = bm as 32bit mantissa exx cp 1 ; if (dexp >= 1) { /* 2 */ jr c,endif2 ld b,a ; bm >>= dexp; shrde: exx srl d rr e exx rr d rr e djnz shrde jr endif4 ; } endif2:

Further calculations need at least 26bits for sign bit and 25th result bit. I use 32bits mantissa. Mantissa alignment of argument 2 mantissa is done next, if needed.

neg ; dexp = 0 - dexp; cp 24 ; if (dexp >= 24) { /* 3 */ jr c,endif3 exx ; return b; push de exx pop hl jp endfn2 ; } endif3:

If argument 2 is much larger then argument 1, argument 2 is returned as result.

exx ld h,0 ; h'l'hl = 32bit mantissa ld d,h ; d'e'de = 32bit mantissa exx cp 1 ; if (dexp >= 1) { /* 4 */ jr c,endif4 ld b,a ; am >>= dexp; shrhl: exx ; srl h rr l exx rr h rr l djnz shrhl exx ld a,b ; save sgn+exp 1 ld b,c ; ae = be; rl b ; roll out sgn 2 rla ; roll in sgn 1 rr b ; roll back exx ; } endif4:

Argument 2 processing is like argument 1 above. Additionally, sgn+exp byte of argument 1 takes sgn from argument 1, but exponent from argument 2.

exx push bc ; copy sgn+exp 1, sgn+exp 2 exx pop bc ; copy sgn+exp 1, sgn+exp 2 ld a,b ; if (as) { /* 5 */ rla ; sgn to carry jr nc,endif5 call neg32 ; am = 0 - am; ; } endif5:

The sign+exp bytes are copied from alternate register set to normal register set. For easy mantissa addition, the argument 1 mantissa is changed into two's complement format, if necessary.

ld a,c ; if (bs) { /* 6 */ rla ; sgn to carry jr nc,endif6 xor a ; bm = 0 - bm; sub e ld e,a ld a,0 sbc a,d ld d,a exx ld a,0 sbc a,e ld e,a ld a,0 sbc a,d ld d,a exx ; } endif6:

Argument 2 mantissa is changed into two's complement format, is necessary, too.

add hl,de ; am += bm; exx adc hl,de exx

Mantissa addition is easy for 8bit "number cruncher" Z80.

ld a,l ; if (0 == am) { /* 7 */ or h exx or l or h exx jr z,endfn1 ; return 0.0; ; }

Mantissa result zero is a special case, because normalized mantissa has always the most significant bit set. By "chance", the coding of signed long zero is the same as float zero.

res 7,b ; as = 0; exx ; if (am < 0) { /* 8 */ bit 7,h exx jr z,endif8 set 7,b ; as = 1; call neg32 ; am = 0 - am; ; } endif8:

Mantissa addition result is converted to sign and magnitude, if necessary. The result sign is set accordingly in the result sgn+exp byte, the former argument 1 sgn+exp byte.

ex de,hl ; hlde = h'l'hl exx push hl exx pop hl bit 0,h ; if (am >= 0x1000000) { /* 9 */ jr z,endif9 srl h ; am >>= 1; rr l rr d rr e inc b ; ++ae; ; } endif9:

First, the mantissa result is copied to normal register set, as requested by Hi-Soft C runtime. Second is test for mantissa overflow.

ld a,b ; if exp positive overflow cp 80h jr nz,endif10 ld hl,07FFFh ; return +infinite jr endfn3 endif10: or a ; if exp negative overflow jr nz,endif11 ld hl,0FFFFh ; return -infinite endfn3: ld de,0FFFFh jr endfn2 endif11:

These two tests handle overflow. Register B holds sgn+exp. Positive exponent overflow happens with register B value of 080h, negative overflow with value zero.

and 07fh ; remove sgn wh1: bit 7,l ; while (am < 0x800000) { jr nz,endwh1 sla e ; am <<= 1; rl d rl l dec b ; --ae; dec a jr wh1 ; } endwh1: ld h,b ; return fp2float(as, am, ae);

After "mantissa cancellation", the result mantissa needs normalization and exponent needs decrement to compensate. Register B has sgn+exp, register A has only exponent. Both registers are used as "counters".

dec a ; if exp underflow jp p,endfn2 xor a ; return zero ld e,a ld d,a ld l,a ld h,a jr endfn2

This part is tricky. We need a test for register A is below or equal zero. Because we decrement register A, the test is now A is below zero. A "jump if positive" is fitting "jump away" opcode.

endfn1: ex de,hl ; hlde = h'l'hl exx push hl exx pop hl ;FADD.C: 7: } endfn2: jp cret ; return float HLDE f1 equ 0

Some function exits needs copy of result float from H'L'HL registers to Hi-Soft C runtime float return registers.

;================================================== ; signed long negate routine ; h'l'hl = 0 - h'l'hl ; needs register a, changes flags ; neg32: xor a sub l ld l,a ld a,0 sbc a,h ld h,a exx ld a,0 sbc a,l ld l,a ld a,0 sbc a,h ld h,a exx ret

The 32bit negate subroutine is needed for argument 1 and result. Having a subroutine instead of inline code saves some program space.

The test-driver for overflow and underflow is program tfadd3.c.

/* tfadd3.c */ unsigned long al[] = { 0x7E800000L, 0x7F800000L, 0xFE800000L, 0xFF800000L, 0x02C00000L, 0x01C00000L, 0x82800000L, 0x81800000L, 0x58FFFFFFL, 0xD8800000L }; unsigned long bl[] = { 0x7E800000L, 0x7F800000L, 0xFE800000L, 0xFF800000L, 0x82800000L, 0x81800000L, 0x02C00000L, 0x01C00000L, 0xD8FFFFFEL, 0x58800001L }; int main() { static char as[16], bs[16], cs[16]; int i; for (i=0; i < 10; ++i) { FL a, b, c; a.l = al[i]; b.l = bl[i]; c.f = fadd(a.f, b.f); printf("0x%08lx = 0x%08lx + 0x%08lx\n", c.l, a.l, b.l); printf("%14.7e = %14.7e + %14.7e\n", a.f + b.f, a.f, b.f); float2asc(as, a.f); float2asc(bs, b.f); float2asc(cs, c.f); printf("%14s = %14s + %14s\n", cs, as, bs); } }

Compile and link the test-driver with:

c tfadd3.c fadd.as a2f7.as -LF

The results are:

C>tfadd3 0x7F800000 = 0x7E800000 + 0x7E800000 4.6106252e+18 = 2.3053126e+18 + 2.3053126e+18 4611686e12 = 2305843e12 + 2305843e12 0x7FFFFFFF = 0x7F800000 + 0x7F800000 -0.0000000e+00 = 4.6106252e+18 + 4.6106252e+18 9223371e12 = 4611686e12 + 4611686e12

The first row is float numbers in hexadecimal. Second row is Hi-Soft radix conversion from float to ASCII and result of Hi-Soft float addition. Third row is my Z80 assembler radix conversion and float addition. Every test case produces these three rows. First test case is float addition without overflow, second test case with positive overflow. The Hi-Soft radix conversion has inaccuracies.

0xFF800000 = 0xFE800000 + 0xFE800000 -4.6106252e+18 = -2.3053126e+18 + -2.3053126e+18 -4611686e12 = -2305843e12 + -2305843e12 0xFFFFFFFF = 0xFF800000 + 0xFF800000 -0.0000000e+00 = -4.6106252e+18 + -4.6106252e+18 -9223371e12 = -4611686e12 + -4611686e12

These test cases handle negative overflow. The Hi-Soft radix conversion has inaccuracies.

0x01800000 = 0x02C00000 + 0x82800000 5.4210064e-20 = 1.6263022e-19 + -1.0842013e-19 5421011e-26 = 16263032e-26 + -10842022e-26 0x00000000 = 0x01C00000 + 0x81800000 0.0000000e+00 = 8.1315110e-20 + -5.4210064e-20 0e0 = 8131516e-26 + -5421011e-26 0x01800000 = 0x82800000 + 0x02C00000 5.4210064e-20 = -1.0842013e-19 + 1.6263022e-19 5421011e-26 = -10842022e-26 + 16263032e-26 0x00000000 = 0x81800000 + 0x01C00000 0.0000000e+00 = -5.4210064e-20 + 8.1315110e-20 0e0 = -5421011e-26 + 8131516e-26

These four test cases handle underflow. Again, the Hi-Soft radix conversion has inaccuracies.

0x41800000 = 0x58FFFFFF + 0xD8FFFFFE 2.0000000e+00 = 1.6776893e+07 + -1.6776892e+07 10000000e-7 = 16777215e0 + -16777214e0 0x41800000 = 0xD8800000 + 0x58800001 2.0000000e+00 = -8.3884472e+06 + 8.3884480e+06 10000000e-7 = -8388608e0 + 8388609e0

At these mantissa cancellation tests the Hi-Soft float addition has inaccuracies, too.

Z80 floating point subtraction

Floating point subtraction is very cheap. Just flip argument 2 mantissa sign and call the floating point addition subroutine. See file fsub.as:

;FSUB.C: 3: float fsub(a, b) ;FSUB.C: 4: register double a, b; ;FSUB.C: 5: { psect text global _fsub, fadd2 _fsub: global ncsv, cret, indir call ncsv defw f1 ;FSUB.C: 6: return a - b; ld a,(ix+3+10) ; flip argument 2 xor 80h ; mantissa sign ld (ix+3+10),a jp fadd2 ;FSUB.C: 7: } f1 equ 0

The "call ncsv" sets up the frame pointer. The sign+exponent byte of argument 2 is on frame pointer location IX+13. Bit 7 of this byte, the mantissa sign bit, is changed and the modified byte is put back. Jump to proper addition subroutine entry point for mission accomplished.

Compile and link the test-driver with:

c tfsub2.c fadd.as fsub.as a2f7.as -LF

Z80 floating point multiplication

Floating point multiplication of two numbers is done as multiply the two normalized mantissas, add the two exponents and xor (exclusive or) the two mantissa signs. Special cases are underflow to minimum and overflow to maximum exponent value.
The following C Header and source code files are used as start for producing optimized Z80 assembler code:

/* fmul.h */ extern float fmul(double, double);

Note: Hi-Soft C compiler has a little bug with ANSI C prototype. Type double and float are both 32bit. Only type double is valid as prototype argument.
The C source:

/* fmul.c */ #include "fmul.h" float fmul(a, b) double a, b; { return a * b; }

Note: Hi-Tech C compiler float and double are the same, both are 32bits. If type is float, the compiler emits "float param coerced to double (warning)". These old C compilers aren't well tested in the floating point area.

The optimized assembler version of fmul.c is in file fmul.as.
The core of floating point multiplication is mantissa multiplication. The mantissa length is 24bit. Therefore we need a 24bit*24bit=48bit multiplication. The two input arguments need 3 registes each, the result occupies 6 registers. The optimized multiplication algorithm needs only 9 registers plus 1 register for loop counter, because 3 registers are used "dual purpose" for one argument and part of the result. I discuss the algorithm in steps.

;================================================== ; unsigned multiply 48bit=24bit*24bit prd = mltr * mltd ; AHL Carry = L'B'C' * CDE ; needs register B, changes flags ; does not change D'H' (sign+exp of float) ; u24mul: xor a ; u24 prdh = 0; ld l,a ld h,a ld b,25 ; char cnt = 25; jr strt
The two input arguments use registers L'B'C' and CDE. Register L' and other registers with ' are part of the alternate register set. The result registers reuse registers L'B'C' for the lower part of product. The upper part uses registers AHL. The register A is the 8bit accumulator, the registers HL are a limited 16bit accumulator. This is optimized use of Z80 registers. Another optimized use is register B for counter.
The product upper 24bits registers AHL are loaded with value zero. The loop counter register B is loaded with 25 and the program jumps to the algorithm entry point. This entry point is not-structured in the middle of the do-while loop. Yeah, all rules are off deep down in assembler land.

do1: ; do { jr nc,endi1 ; if (carry) { add hl,de ; prdh += mltd; adc a,c endi1: ; }

Multiplication by hand is done as "shifted, conditional addition". This is done here. The carry flag gives the condition. If there was an 1 bit in the shifted argument, first a 16bit add is done, then an 8bit add.

rra ; prdh >>= 1; rr h rr l

A carry from the above addition and the upper 24bits of product are shifted right. The pseudo C comment does not reflect all details of the assembler code.

strt: exx ; carry = mltr.lsb; mltr >>= 1; rr l rr b rr c exx

A carry from the shift of the upper 24bits of product and the lower 24bits of product are shifted right. The lower 24bits of product and the multiplier use the same registers. The lower product is shifted in from the carry to the most significant bit, the multiplier is shifted out from the least significant bit to the carry.

djnz do1 ; } while (--cnt > 0); exx rl l ; carry = bit 25 exx ret

The do-while loop uses the "decrement and jump if not zero" Z80 opcode. The product 25th bit is copied to carry flag. Last opcode is "return from subroutine".
I got inspiration for u24mul register allocation from the Dave Nutting Associates (DNA) Z80 H floating point package from 1978.

The C runtime compatible subroutine _fmul starts with:

; fmul.as ;FMUL.C: 2: extern float fmul(double, double); ;FMUL.C: 4: float fmul(a, b) ;FMUL.C: 5: double a, b; ;FMUL.C: 6: { psect text global _fmul _fmul: global ncsv, cret, indir call ncsv defw f2 ;FMUL.C: 7: return a * b; ld l,(ix+6) ld h,(ix+1+6) ld e,(ix+10) ld d,(ix+1+10) exx ld l,(ix+2+6) ld h,(ix+3+6) ld e,(ix+2+10) ld d,(ix+3+10) exx

;================================================== ; float multiply routine ; hlde = h'l'hl * d'e'de ; needs registers a, b, c, b', c', changes flags ; fmul: push hl ; multiplier low+mid exx pop bc ; multiplier low+mid ld a,e ; multiplicand high exx ld c,a ; multiplicand high call u24mul ; AHL Carry = L'B'C' * CDE

The label fmul is the assembler (values in registers) entry of the fmul subroutine. The register values get arranged for the u24mul mantissa multiplication subroutine.

rr c ; Bit 7 = carry ex de,hl ; save to result mantissa bytes ld l,a ld b,64 ; exp_bias = 64; /* 1 */ or a ; if (0 == prd.msb) { jp m,endi3 sla c ; prd <<= 1; rl e rl d rl l inc b ; ++exp_bias; /* 2 */ endi3: ; }

Some results need a one bit shift left for normalization. The 25th bit to avoid precision loss is copied in the carry flag from the u24mul subroutine. The C runtime expects the return value in registers HLDE with H contains the mantissa sign plus exponent byte. The "ex de,hl" is faster and saves space compared to two "ld" opcodes.
The normalized mantissa values are between 0x800000 and 0xFFFFFF. The result of mantissa multiplication is therefore between 0x400000000000 and 0xFFFFFE000001. We need only the upper 24bit, because we did a fraction multiplication (exactly a Q 1.23 times Q 1.23 multiplication). As with radix conversion, a mantissa shift needs an exponent change to compensate or to have the same information in another "packaging". See comment 2.

ld a,b ; copy exp_bias exx ld b,a ; copy exp_bias ld a,d ; exp2 = sign_exp2 & 0x7F; and 07Fh ld e,a ; copy exp2 ld a,h ; exp1 = sign_exp1 & 0x7F; and 07Fh sub b ; exp = exp1 - exp_bias + exp2; /* 3 */ add a,e common: push af ; /* save exp, flags */

The exponent is biased. We could transform the two exponents from biased notation to two's exponent notation, do the addition, do the underflow/overflow correction and transform back to biased notation. Or we do it in biased notation to save some program space and execution time.
First of all, we have to get rid of mantissa sign with "and 07Fh" opcode. Second we have to get rid of one bias value. Above we loaded register B with value 64 or 65, see comments 1 and 2. This is the bias value. Opcode "sub b" removes this bias value, see comment 3. Last, we add the two "prepared" exponent values and save result and flags on stack.
From label common on, the fmul and fdiv post processing is the same.

ld a,h ; sign = sign_exp1 ^ sign_exp2; xor d ; /* sign (and garbage) */ exx ld h,a ; copy result sign

Next part is calculating result sign as exclusive or of the two arguments signs.

pop af ; if (1 == exp.msb) { jp p,endi4 cp 191 ; if (exp < 191 ) { /* 4 */ jr c,else5 xor a ; exp = 0; /* underflow value */ ld e,a ; man = 0; ld d,a ld l,a jr endi5 else5: ; } else { ld a,127 ; exp = 127; /* overflow value */ ld de,0FFFFh ; man = 0xFFFFFF; ld l,e endi5: ; } endi4: ; }

The biased exponent underflow/overflow correction needs a value that separates underflow from overflow. The biased exponent underflow is below 0, overflow is above 127. The border between underflow and overflow is half way between 127 and 0 (256), is 191. The underflow exponent in biased notation is 0, underflow mantissa is 0. The overflow exponent is 127, overflow mantissa is 0xFFFFFF.

rla ; roll out bit 7 exp byte rl h ; roll in sign bit rra ; roll back bit 7 ld h,a ; save to result sign+exp byte ;FMUL.C: 8: } jp cret ; return float in HLDE f2 equ 0

Some (clever) rolling of bit 7 to carry flag, change this carry flag to the sign bit and roll back carry flag to bit 7 does the job. The "jump cret" is part of C runtime and - I assume - cleans the stack frame before doing the return from subroutine.

The "test-driver" for file fmul.as is:

/*tfmul.c */ #include <stdio.h> #include "fmul.h" typedef union { float f; unsigned long l; } FL; unsigned long al[] = { 0x40800000L, 0xC0FFFFFFL, 0x40800000L, 0xC0FFFFFFL, 0x00FFFFFFL, 0x01800000L, 0x21800000L, 0x5F800000L, 0x60800000L, 0x7F800000L, 0x7F800000L, 0x00000000L}; unsigned long bl[] = { 0x40800000L, 0x40800000L, 0xC0FFFFFFL, 0xC0FFFFFFL, 0x00FFFFFFL, 0x01800000L, 0x21800000L, 0x5F800000L, 0x60800000L, 0x7F800000L, 0xFF800000L, 0x00000000L}; int main() { int i; for (i = 0; i < 12; ++i) { FL a, b, c; a.l = al[i]; b.l = bl[i]; c.f = a.f * b.f; printf(" 0x%08lx %13e = %13e * %13e\n", c.l, c.f, a.f, b.f); c.f = fmul(a.f, b.f); printf("fmul 0x%08lx ", c.l); printf("%13e = 0x%08lx * 0x%08lx\n", c.f, a.l, b.l); } }

Compile test-driver in C and fmul in assembler with:

c tfmul.c fmul.as -LF

The output is:

0x3F800000 2.500000e-01 = 5.000000e-01 * 5.000000e-01 fmul 0x3F800000 2.500000e-01 = 0x40800000 * 0x40800000 0xBFFFFFFF -4.999998e-01 = -9.999997e-01 * 5.000000e-01 fmul 0xBFFFFFFF -4.999998e-01 = 0xC0FFFFFF * 0x40800000 0xBFFFFFFF -4.999998e-01 = 5.000000e-01 * -9.999997e-01 fmul 0xBFFFFFFF -4.999998e-01 = 0x40800000 * 0xC0FFFFFF 0x40FFFFFE 9.999996e-01 = -9.999997e-01 * -9.999997e-01 fmul 0x40FFFFFE 9.999996e-01 = 0xC0FFFFFF * 0xC0FFFFFF

The first four test cases test the mantissa normalization and the mantissa sign handling. The first row is Hi-Soft C runtime multiplication, the second row marked "fmul" is my multiplication subroutine. The results are the same.

0x00000000 0.000000e+00 = 0.000000e+00 * 0.000000e+00 fmul 0x00000000 0.000000e+00 = 0x00FFFFFF * 0x00FFFFFF 0x00000000 0.000000e+00 = 5.421006e-20 * 5.421006e-20 fmul 0x00000000 0.000000e+00 = 0x01800000 * 0x01800000 0x01800000 5.421006e-20 = 2.328306e-10 * 2.328306e-10 fmul 0x01800000 5.421006e-20 = 0x21800000 * 0x21800000
Next three test cases check exponent underflow. The exponent value 0 seems to have Hi-Tech C runtime interpretation "number is 0.0e0". The results are the same.

0x7D800000 1.152656e+18 = 1.073680e+09 * 1.073680e+09 fmul 0x7D800000 1.152656e+18 = 0x5F800000 * 0x5F800000 0x7F800000 4.610625e+18 = 2.147360e+09 * 2.147360e+09 fmul 0x7F800000 4.610625e+18 = 0x60800000 * 0x60800000 0x00000000 0.000000e+00 = 4.610625e+18 * 4.610625e+18 fmul 0x7FFFFFFF 9.221073e+18 = 0x7F800000 * 0x7F800000 0x00000000 0.000000e+00 = 4.610625e+18 * -4.610625e+18 fmul 0xFFFFFFFF -9.221073e+18 = 0x7F800000 * 0xFF800000
Next four cases check exponent overflow. There are differences. Hi-Tech C runtime "overflows" to 0.0e0, my fmul overflows to maximum exponent, maximum mantissa value.

0x00000000 0.000000e+00 = 0.000000e+00 * 0.000000e+00 fmul 0x00000000 0.000000e+00 = 0x00000000 * 0x00000000
The last case is 0.0e0. The Hi-Tech printf float C runtime crashes with value 0x7F000000, that is mantissa equal zero and exponent not equal zero.

Note: One could add an overflow "hook" in the fmul subroutine to abort program execution. Working on with "infinite" numbers will not produce usable values. Underflow is an error condition, too.

Z80 32bit unsigned multiplication

The Sinclair ZX81 and ZX Spectrum have 40bit floating point numbers with 32bit mantissa. The result of two normalized mantissas can range from 0.25 to 0.999..

; mul32.z80 ;================================================== ; unsigned multiply routine 64bit=32bit*32bit ; H'L'HLB'C'BC = D'E'DE * B'C'BC ; needs register A, changes flags ; mul32: xor a ; load zero, reset carry flag ld l,a ; Initialise HL to zero for the result. ld h,a exx ld l,a ; Also initialise H'L' for the result. ld h,a exx ld a,b ; free B for loop counter ld b,33 ; B counts 33 decimal, Hex.21, shifts. jr strtmlt ; Jump forward into the loop. mltloop: ; Now enter the multiplier loop. jr nc,noadd ; Jump forward to NOADD if no carry, ; i.e. the multiplier bit was reset. add hl,de ; Else, add the multiplicand in exx ; D'E'DE into adc hl,de ; the result being built up on exx ; H'L'HL. noadd: exx ; Whether multiplicand was added rr h ; or not, shift result right in rr l ; H'L'HL, i.e. the shift is done by exx ; rotating each byte with carry, so rr h ; that any bit that drops into the rr l ; carry is picked up by the next ; byte, and the shift continued ; into B'C'AC. strtmlt: exx ; Shift right the multiplier in rr b ; B'C'AC. rr c ; A final bit dropping into the exx ; carry will trigger another add of rra ; the multiplicand to the result. rr c djnz mltloop ; Loop 33 times to get all the bits. ld b,a ; restore B ret

The comments are from the book The Complete Spectrum ROM Disassembly by Ian Logan and Frank O'Hara. I present a little variation of the original Spectrum code. The algorithm structure is simple and elegant. One counter loop, one if. The minimum structure for an useful algorithm.

; 0xFFFFFFFF * 0xFFFFFFFF = 0xFFFFFFFE00000001 ; 0x80000000 * 0x80000000 = 0x4000000000000000

The first two rows show results for multiply two maximum normalized numbers and multiply two minimum normalized numbers. The second result is not a normalized number.

; 0x80000000 * 0x80000001 = 0x4000000080000000 ; 0x80000001 * 0x80000000 = 0x4000000080000000

These two rows show that normalization shift should include top 33bits. The normalized result is 0x80000001*2^-1.

; 0xC0000001 * 0xBFFFFFFF = 0x8FFFFFFFFFFFFFFF ; 0xBFFFFFFF * 0xC0000001 = 0x8FFFFFFFFFFFFFFF

The last two rows show that rounding should be done. Rounding value is 0x80000000, that is shifted 0.5 of last digit. After adding result is 0x900000007FFFFFFF. Truncation result is 0x90000000.

Z80 floating point division

Division and multiplication are twins for pre- and post-processing. The core of multiplication is addition, the core of division is subtraction. For every bit of the multiplicand, the algorithm performs one addition or nothing. For every bit of the divisor, the algorithm performs one subtraction, which is undone by an addition in case of carry set. This is the main reason why division is slower then multiplication.
The two normalized arguments can range from 0.5 to 0.999...

; u24div.z80 ;================================================== ; unsigned divide 25bit=24bit/24bit 2*q = n / d ; L'B'C' Carry = AHL / CDE ; changes flags ; does not change D'H' (sign+exp of float) ; u24div: ld b,25 ; char cnt = 25; jr else1

The subroutine calculates 2*q, because the quotient of 0.999.. / 0.5 = 1.999... or 0xFFFFFF / 0x800000 = 0x1FFFFFF is not normalized. The result range is 0.25 to 0.999... or 0x400000 to 0xFFFFFF. The result before normalization should be 25bits to have always 24bits precision after normalization. The carry flag is used as quotient 25th bit.

do1: ; do { exx ; q += q + carry; rl c rl b rl l exx

The quotient in registers L'B'C' is shifted left. The quotient is build up from least significant bit to most significant bit.

add hl,hl ; carry = n.msb; n += n; adc a,a jr nc,else1 ; if (carry) { /* without restore */ or a ; n -= d; sbc hl,de sbc a,c scf ; carry = 1; jr endi1

The nominator in registers AHL is shifted left. This shift can set carry flag. In this case, the dividend is larger then the divisor. This is the "without restore" case. The nominator denominator subtraction is done, the carry flag is set because the quotient bit shall be set.

else1: ; } else { /* with restore */ or a ; carry = n < d; n -= d; sbc hl,de sbc a,c jr nc,endi2 ; if (carry) { /* restore */ add hl,de ; n += d; adc a,c endi2: ; } ccf ; carry = !carry; endi1: ; }

The second case is "with restore". The nominator denominator subtraction sets the carry flag, if the nominator is less then the denominator. Then the subtraction is undone with an addition. No carry after subtraction results in a set bit in the quotient. The "complement carry flag" opcode CCF does this job.

djnz do1 ; } while (--cnt > 0); ; carry = bit 25; ret

The final steps are conditional jump to the begin of the do-while loop and return from subroutine. The DJNZ opcode does not change flags.
The entry point into the do-while loop is label else1. This is no more structured programming. I use a variation of the Sinclair ZX81 and ZX Spectrum unsigned long 32bit division in The Complete Spectrum ROM Disassembly.

; n, AHL d, CDE q,L'B'C' Carry ; 0x800000 / 0xFFFFFF = 0x400000 0 ; 0x800000 / 0xFFFFFE = 0x400000 1 ; 0x800000 / 0xFFFFFD = 0x400000 1 ; 0x800000 / 0xFFFFFC = 0x400001 0 ; 0x800000 / 0xFFFFFB = 0x400001 0 ; 0xFFFFFF / 0xFFFFFF = 0x800000 0 ; 0xFFFFFF / 0xFFFFFE = 0x800000 1 ; 0xFFFFFF / 0xFFFFFD = 0x800001 0 ; 0xFFFFFF / 0xFFFFFC = 0x800001 1 ; 0xFFFFFF / 0xFFFFFB = 0x800002 0 ; 0x800000 / 0x800004 = 0x7FFFFC 0 ; 0x800000 / 0x800003 = 0x7FFFFD 0 ; 0x800000 / 0x800002 = 0x7FFFFE 0 ; 0x800000 / 0x800001 = 0x7FFFFF 0 ; 0x800000 / 0x800000 = 0x800000 0 ; 0xFFFFFF / 0x800004 = 0xFFFFF7 0 ; 0xFFFFFF / 0x800003 = 0xFFFFF9 0 ; 0xFFFFFF / 0x800002 = 0xFFFFFB 0 ; 0xFFFFFF / 0x800001 = 0xFFFFFD 0 ; 0xFFFFFF / 0x800000 = 0xFFFFFF 0

The hexadecimal number 0x800000 has interpretation 0.5 as Q 0.24 number, that is 0 bits before binary point and 24 bits after binary point. Hexadecimal 0xFFFFFF is 0.999...

; fdiv.as ;fdiv.h: 2: extern float fdiv(double, double); ;FDIV.C: 4: float fdiv(a, b) ;FDIV.C: 5: double a, b; ;FDIV.C: 6: { psect text global _fdiv _fdiv: global ncsv, cret, indir call ncsv defw f2 ;FDIV.C: 7: return a / b; ld l,(ix+6) ld h,(ix+1+6) ld e,(ix+10) ld d,(ix+1+10) exx ld l,(ix+2+6) ld h,(ix+3+6) ld e,(ix+2+10) ld d,(ix+3+10) exx ;================================================== ; float divide routine ; hlde = h'l'hl * d'e'de ; needs registers a, b, c, b', c', changes flags ; fdiv: exx ; arguments moving ld a,e ; divisor high exx ld c,a ; divisor high exx ld a,l ; dividend high exx call u24div ; L'B'C' Carry = AHL / CDE

The arguments are copied from the stack frame to registers H'L'HL and D'E'DE. Then the arguments are "moved around" to fit the u24div subroutine requirements.

rr c ; Bit 7 = carry exx push bc ; quotient low+mid ld a,l ; quotient high exx pop de ; quotient low+mid ld l,a ld b,65 ; exp_bias = 65; /* 1 because 2*q */ or a ; if (0 == prd.msb) { jp m,endi3 sla c ; prd <<= 1; rl e rl d rl l dec b ; --exp_bias; /* 2 because exp1 - exp2 */ endi3: ; } ld a,b ; copy exp_bias exx ld b,a ; copy exp_bias ld a,d ; exp2 = sign_exp2 & 0x7F; and 07Fh ld e,a ; copy exp2 ld a,h ; exp1 = sign_exp1 & 0x7F; and 07Fh sub e ; exp = exp1 - exp2 + exp_bias; /* 3 */ add a,b jp common

The post processing for fdiv is similar to fmul with differences. The init value of exp_bias is 65, because of the u24div subroutine, see comment 1. If the most significant bit of the quotient is zero, the exp_bias is decremented, see comment 2. Last difference is division needs subtraction of both exponents, see comment 3. The last part of post processing is common. See assembler code in file fmul.as above.

The test-driver is:

/* tfdiv.c */ #include <stdio.h> #include "fdiv.h" typedef union { float f; unsigned long l; } FL; unsigned long al[] = { 0x41800000L, 0xC0800000L, 0x3F800000L, 0xC1800000L, 0x40800000L, 0x3F800000L, 0x5F800000L, 0x60800000L, 0x20800000L, 0x1F800000L, 0x00000000L, 0x41800000L, 0xC1800000L}; unsigned long bl[] = { 0x40800000L, 0x40800000L, 0xC0800000L, 0xBFFFFFFFL, 0x3FFFFFFFL, 0x3FFFFFFFL, 0x21800000L, 0x20800000L, 0x60800000L, 0x61800000L, 0x41800000L, 0x00000000L, 0x00000000L}; int main() { int i; for (i = 0; i < 13; ++i) { FL a, b, c; a.l = al[i]; b.l = bl[i]; c.f = a.f / b.f; printf(" 0x%08lx %13e = %13e / %13e\n", c.l, c.f, a.f, b.f); c.f = fdiv(a.f, b.f); printf("fdiv 0x%08lx ", c.l); printf("%13e = 0x%08lx / 0x%08lx\n", c.f, a.l, b.l); } }

The header file is:

/* fdiv.h */ extern float fdiv(double, double);

The Hi-Soft compiler creates the program with:

c tfdiv.c fdiv.as -LF

The output is:

C>tfdiv 0x42800000 2.000000e+00 = 1.000000e+00 / 5.000000e-01 fdiv 0x42800000 2.000000e+00 = 0x41800000 / 0x40800000 0xC1800000 -1.000000e+00 = -5.000000e-01 / 5.000000e-01 fdiv 0xC1800000 -1.000000e+00 = 0xC0800000 / 0x40800000 0xC0800000 -5.000000e-01 = 2.500000e-01 / -5.000000e-01 fdiv 0xC0800000 -5.000000e-01 = 0x3F800000 / 0xC0800000 0x42800001 2.000000e+00 = -1.000000e+00 / -4.999998e-01 fdiv 0x42800000 2.000000e+00 = 0xC1800000 / 0xBFFFFFFF 0x41800001 1.000000e+00 = 5.000000e-01 / 4.999998e-01 fdiv 0x41800000 1.000000e+00 = 0x40800000 / 0x3FFFFFFF 0x40800001 5.000000e-01 = 2.500000e-01 / 4.999998e-01 fdiv 0x40800000 5.000000e-01 = 0x3F800000 / 0x3FFFFFFF

These six test cases test sign handling and mantissa shift handling. The rows with "fdiv" use fdiv subroutine, the rows without use Hi-Soft C runtime. The differences are very small.

0x7F800000 4.610625e+18 = 1.073680e+09 / 2.328306e-10 fdiv 0x7F800000 4.610625e+18 = 0x5F800000 / 0x21800000 0x81800000 -5.421006e-20 = 2.147360e+09 / 1.164153e-10 fdiv 0x7FFFFFFF 9.221073e+18 = 0x60800000 / 0x20800000

Division overflow handling is different.

0x01800000 5.421006e-20 = 1.164153e-10 / 2.147360e+09 fdiv 0x01800000 5.421006e-20 = 0x20800000 / 0x60800000 0xFF800000 -4.610625e+18 = 5.820764e-11 / 4.294720e+09 fdiv 0x00000000 0.000000e+00 = 0x1F800000 / 0x61800000

Division underflow handling is different, too.

0x00000000 0.000000e+00 = 0.000000e+00 / 1.000000e+00 fdiv 0x00000000 0.000000e+00 = 0x00000000 / 0x41800000

A zero as dividend (numerator) has zero as result.

0x83800000 -2.168403e-19 = 1.000000e+00 / 0.000000e+00 fdiv 0x7FFFFFFF 9.221073e+18 = 0x41800000 / 0x00000000 0x83800000 -2.168403e-19 = -1.000000e+00 / 0.000000e+00 fdiv 0xFFFFFFFF -9.221073e+18 = 0xC1800000 / 0x00000000 A zero as divisor (denominator) produces positive or negative infinite as result. The Hi-Soft C runtime produces strange results. All in all, my fdiv subroutine has better corner cases handling.
Note: Another solution for div/0 is program abort.

68000 32bit unsigned division

The Alycon C compiler unsigned long divide subroutine is faulty, see above. I wrote a 68000 assembler routine that is based on Dave Nutting Associates Z80 and Sinclair Z80 assembler solutions. It uses opcodes that are special to 68000 for fast execution.
The subroutine calculates 2*q, because the result of 0.999.. / 0.5 = 1.999... or 0xFFFFFFFF / 0x80000000 = 0x1FFFFFFFF is not normalized. The result range is 0.25 to 0.999... or 0x40000000 to 0xFFFFFFFF. The result before normalization should be 33bits to have always 32bits precision after normalization.

; div33.x68 ;================================================== ; unsigned divide routine 33bit=32bit/32bit 2*q = n / d ; D0.L D1.B = D7.L / D6.L ; Bit 33 = D1 bit 0 ; needs register D2, changes flags ; div32: ; char qflag; moveq #32,D2 ; short cnt = 32; bra.s else1 do1: ; do { add.b D1,D1 ; xflag = qflag; addx.l D0,D0 ; q += q + xflag; add.l D7,D7 ; carry = n.msb; n += n; bcc.s else1 ; if (carry) { /* without restore */ sub.l D6,D7 ; n -= d; moveq #-1,D1 ; qflag = -1; bra.s endi1 else1: ; } else { /* with restore */ sub.l D6,D7 ; carry = n < d; n -= d; bcc.s endi2 ; if (carry) { /* restore */ add.l D6,D7 ; n += d; endi2: ; } scc D1 ; qflag = !carry; endi1: ; } dbra D2,do1 ; } while (--cnt >= 0); rts

The algorithm shifts the nominator in register D7 left. The carry flag and xflag, a 68000 specific flag, get set if the most significant bit of D7 was set before shift. In this case, the nominator minus denominator subtraction is done without restore and qflag is set. The variable qflag is in register D1. I use register D1, because xflag opcodes like "ORI.B #$10,CCR" are slow.
If shift of nominator does not set carry flag, the restoring subtraction is done in the else part of the algorithm. The special 68000 opcode "SCC" loads the value 0xFF to register if carry was clear or value 0x00 otherwise. Older CPUs like 6502 or Z80 don't have these store flags to registers opcodes.
The "ADD.B D1,D1" opcode copies the value of qflag to xflag before the quotient gets shifted. The qflag is also the 33th bit of the quotient after the do-while loop terminates.
The entry point into the do-while loop is label else1. This is no more structured programming. Unfortunately, optimization kills structure. The multiply and divide loops are the narrowest loops in the system. Here, every clock cycle counts.

; n, D7.L d, D6.L q, D0.L D1.B ; 0x80000000 / 0xFFFFFFFF = 0x40000000 0x00 ; 0x80000000 / 0xFFFFFFFE = 0x40000000 0xFF ; 0x80000000 / 0xFFFFFFFD = 0x40000000 0xFF ; 0x80000000 / 0xFFFFFFFC = 0x40000001 0x00 ; 0x80000000 / 0xFFFFFFFB = 0x40000001 0x00 ; 0xFFFFFFFF / 0xFFFFFFFF = 0x80000000 0x00 ; 0xFFFFFFFF / 0xFFFFFFFE = 0x80000000 0xFF ; 0xFFFFFFFF / 0xFFFFFFFD = 0x80000001 0x00 ; 0xFFFFFFFF / 0xFFFFFFFC = 0x80000001 0xFF ; 0xFFFFFFFF / 0xFFFFFFFB = 0x80000002 0x00 ; 0x80000000 / 0x80000004 = 0x7FFFFFFC 0x00 ; 0x80000000 / 0x80000003 = 0x7FFFFFFD 0x00 ; 0x80000000 / 0x80000002 = 0x7FFFFFFE 0x00 ; 0x80000000 / 0x80000001 = 0x7FFFFFFF 0x00 ; 0x80000000 / 0x80000000 = 0x80000000 0x00 ; 0xFFFFFFFF / 0x80000004 = 0xFFFFFFF7 0x00 ; 0xFFFFFFFF / 0x80000003 = 0xFFFFFFF9 0x00 ; 0xFFFFFFFF / 0x80000002 = 0xFFFFFFFB 0x00 ; 0xFFFFFFFF / 0x80000001 = 0xFFFFFFFD 0x00 ; 0xFFFFFFFF / 0x80000000 = 0xFFFFFFFF 0x00

The first row shows that 0.5 / 0.999.. is 0.25 and 33th bit is zero. The following rows show the 33bit precision of this div32 subroutine.

The EASy68K is an editor/assembler/simulator for Motorola 68000.

The following 68000 division subroutine has 34bits precision. The result is again 2*q. The 33rd and 34th quotient bits are bit 1 and bit 0 of register D4.

; div34.x68 ;================================================== ; unsigned divide routine 34bit=32bit/32bit 2*q = n / d ; D0.L D4.B = D7.L / D6.L ; Bit 33 = D4 bit 1, Bit 34 = D4 bit 0 ; needs register D1, D2, D3, changes flags ; div32: ; char qflag; moveq #32,D2 ; short cnt1 = 32; moveq #1,D3 ; short cnt2 = 1; /* for 34th bit */ moveq #0,D4 ; char qbits = 0; bra.s else1 do1: ; do { add.b D1,D1 ; xflag = qflag.msb; addx.l D0,D0 ; q += q + xflag; do2: ; do { /* not structured */ add.l D7,D7 ; carry = n.msb; n += n; bcc.s else1 ; if (carry) { /* without restore */ sub.l D6,D7 ; n -= d; moveq #-1,D1 ; qflag = -1; bra.s endi1 else1: ; } else { /* with restore */ sub.l D6,D7 ; carry = n < d; n -= d; bcc.s endi2 ; if (carry) { /* restore */ add.l D6,D7 ; n += d; endi2: ; } scc D1 ; qflag = !carry; endi1: ; } dbra D2,do1 ; } while (--cnt1 >= 0); add.b D1,D1 ; xflag = qflag.msb; addx.b D4,D4 ; qbits += qbits + xflag; moveq #0,D2 ; cnt1 = 0; /* cnt1 fall through */ dbra D3,do2 ; } while (--cnt2 >= 0); rts This subroutine has a second do-while loop that interlace with the first do-while loop. Again, this code is not structured. The second subroutine needs more clock cycles 2378 vs. 2274 for 0x80000000 / 0xFFFFFFFF.

; n, D7.L d, D6.L q, D0.L D4.B ; 0x80000000 / 0xFFFFFFFF = 0x40000000 0x01 ; 0x80000000 / 0xFFFFFFFE = 0x40000000 0x02 ; 0x80000000 / 0xFFFFFFFD = 0x40000000 0x03 ; 0x80000000 / 0xFFFFFFFC = 0x40000001 0x00 ; 0x80000000 / 0xFFFFFFFB = 0x40000001 0x01 ; 0xFFFFFFFF / 0xFFFFFFFF = 0x80000000 0x00 ; 0xFFFFFFFF / 0xFFFFFFFE = 0x80000000 0x02 ; 0xFFFFFFFF / 0xFFFFFFFD = 0x80000001 0x00 ; 0xFFFFFFFF / 0xFFFFFFFC = 0x80000001 0x02 ; 0xFFFFFFFF / 0xFFFFFFFB = 0x80000002 0x00

6502 24bit unsigned division

The 6502 carry flag has different behavior for addition and subtraction. Before addition you clear carry flag. After addition, a set carry flag signals unsigned overflow. Before subtraction you set carry flag. After subtraction, a reset carry flag signals borrow (minuend is smaller then subtrahend). This opposite behavior of carry for addition and subtraction is beneficial for 6502 unsigned division subroutine.

; u24div.65s ; unsigned divide routine 25bit=24bit/24bit 2*q = n / d ; u24q, u24qx = u24n / u24d ; Bit 25 = u24qx bit 7 ;-------------------------------- u24n = 0 ; unsigned 24bit in: n u24d = u24n+3 ; unsigned 24bit in: d u24q = u24d+3 ; unsigned 24bit out: 2*q = n / d u24qx = u24q+3 ; unsigned char out: 2*q 25th bit = n / d ;-------------------------------- div24: stz u24qx ; char qx = 0; ldy #25 ; char cnt = 25; bra else1 do1: ; do { rol u24q ; q <<= 1; q |= carry; rol u24q+1 rol u24q+2 asl u24n ; carry = n.msb; n <<= 1; rol u24n+1 rol u24n+2 bcc else1 ; if (carry) { /* without restore */ jsr sub24 ; n -= d; sec ; carry = 1; bra endi1 else1: ; } else { /* with restore */ jsr sub24 ; carry = n >= d; n -= d; bcs endi2 ; if (!carry) { /* restore */ jsr add24 ; n += d; clc ; carry = 0; endi2: ; } endi1: ; } dey ; } while (--cnt > 0); bne do1 ror u24qx ; qx.msb = carry; rts

The parameter passing of div24 subroutine is through "well known" memory locations. The subroutines add24 and sub24 are simple and are given in the assembler code file u24div.65s. The 6502 division algorithm is the same as the 68000 above. Flag manipulation is fast on the 6502, not slow as the 68000 opcodes with CCR argument.
The u24div subroutine can easily be expanded to 32bits.

Z80 32bit unsigned division

Adapting the unsigned long divide algorithm to Z80 was easy. The main difference to the 6502 version is the Z80 traditional carry flag handling. If you have borrow in subtraction, that is minuend is smaller then subtrahend, carry flag is set. Therefore we have CCF, complement carry flag, opcode in the assembler code.
My Z80 assembler code is different from the Sinclair ZX81 and ZX Spectrum unsigned long 32bit division in The Complete Spectrum ROM Disassembly. The result (quotient) of two normalized mantissas can range from 0.5 to 1.999.. Both division algorithms calculate 2*q = n / d. Therefore the result is in the range 0.25 to 0.999.. To avoid loss of precision due to normalization shift, the quotient must have 33bits.

; udiv33.z80 ;================================================== ; unsigned divide routine 33bit=32bit/32bit 2*q = n / d ; B'C'ACB = H'L'HL / D'E'DE ; Bit 33 = B bit 7 ; changes flags ; div32: ld b,33 ; char cnt = 33; jr else1 do1: ; do { rl c ; q <<= 1; q |= carry; rla exx rl c rl b exx add hl,hl ; carry = n.msb; n += n; exx adc hl,hl exx jr nc,else1 ; if (carry) { /* without restore */ or a ; n -= d; sbc hl,de exx sbc hl,de exx scf ; carry = 1; jr endi1 else1: ; } else { /* with restore */ or a ; carry = n < d; n -= d; sbc hl,de exx sbc hl,de exx jr nc,endi2 ; if (carry) { /* restore */ add hl,de ; n += d; exx adc hl,de exx endi2: ; } ccf ; carry = !carry; endi1: ; } djnz do1 ; } while (--cnt > 0); rr b ; qx.msb = carry; ret

The comments are pseudo C language. Pseudo because the assembler code is not structured, we have a jump into the middle of an if-else statement.

The Z80DT MS-DOS program is an editor/assembler/simulator/download tool for Z80, specially for MPF-1B Micro-Professor board.

; n, H'L'HL d, D'E'DE q, B'C'AC B ; 0x80000000 / 0xFFFFFFFF = 0x40000000 0x00 ; 0x80000000 / 0xFFFFFFFE = 0x40000000 0x80 ; 0x80000000 / 0xFFFFFFFD = 0x40000000 0x80 ; 0x80000000 / 0xFFFFFFFC = 0x40000001 0x00 ; 0xFFFFFFFF / 0xFFFFFFFF = 0x80000000 0x00 ; 0xFFFFFFFF / 0xFFFFFFFE = 0x80000000 0x80 ; 0xFFFFFFFF / 0xFFFFFFFD = 0x80000001 0x00 ; 0xFFFFFFFF / 0xFFFFFFFC = 0x80000001 0x80 ; 0x80000000 / 0x80000004 = 0x7FFFFFFC 0x00 ; 0x80000000 / 0x80000003 = 0x7FFFFFFD 0x00 ; 0x80000000 / 0x80000002 = 0x7FFFFFFE 0x00 ; 0x80000000 / 0x80000001 = 0x7FFFFFFF 0x00 ; 0xFFFFFFFF / 0x80000004 = 0xFFFFFFF7 0x00 ; 0xFFFFFFFF / 0x80000003 = 0xFFFFFFF9 0x00 ; 0xFFFFFFFF / 0x80000002 = 0xFFFFFFFB 0x00 ; 0xFFFFFFFF / 0x80000001 = 0xFFFFFFFD 0x00

The quotient are between 0.25 and 0.999... for normalized dividend and divisor.
The unsigned long divide algorithm is a little complicated, as we can see at the faulty Alcyon C compiler runtime subroutine.

Summary

In retrospective, the traditional floating point conversion is concise. It is multi-step, but each step is easy. There are some clever change of perspective or clever interpretation "tricks" to do the job. Up to now I did not find a good textbook on this topic - not even in Donald Knuth's masterful "Art of Computer Programming". My paper fills the gap for me, and maybe for you, too.

The Z80 assembler subroutines are "memory lane" for me. I never documented the Z80 assembler tricks of the trade before. Maybe there are still old and new assembler connoisseurs around. Long live 8bit number cruncher Z80.

Appendix A: Ask Deepseek

Question: Convert 9.99e-9 to binary floating point

Answer:

To convert the number $9.99 \times 1 0^{- 9}$ to its binary floating-point representation, we'll follow these steps:

Convert the Decimal to Binary:
- First, convert the decimal number $9.99$ to its binary equivalent.
- The integer part $9$ in binary is $1001$ .
- The fractional part $0.99$ in binary is approximately $0.1111110101110000101000111101011100001010001111010111$ (repeating).
Combine the Integer and Fractional Parts:
- Combine the integer and fractional parts to get the binary representation of $9.99$ :
  $1001.1111110101110000101000111101011100001010001111010111$
Normalize the Binary Number:
- Normalize the binary number to the form $1. x x x x \times 2^{e}$ :
  $1.0011111110101110000101000111101011100001010001111010111 \times 2^{3}$
Adjust the Exponent:
- Since the original number is $9.99 \times 1 0^{- 9}$ , we need to adjust the exponent accordingly.
- The exponent for $1 0^{- 9}$ in binary is approximately $- 30$ (since $2^{- 30} \approx 9.31 \times 1 0^{- 10}$ ).
Combine the Adjusted Exponent with the Mantissa:
- The adjusted exponent is $- 30$ , and the mantissa is the normalized binary number without the leading 1.
Convert to IEEE 754 Format:
- For a 64-bit double-precision floating-point number:
  - Sign bit: 0 (positive number)
  - Exponent: $- 30 + 1023 = 993$ (in 11 bits: $1111100001$ )
  - Mantissa: The first 52 bits of the normalized mantissa.
Final Binary Representation:
- Combine the sign bit, exponent, and mantissa to get the final 64-bit binary floating-point representation.

Final Answer:

0 01111100001 0011111110101110000101000111101011100001010001111011

This is the 64-bit binary floating-point representation of $9.99 \times 1 0^{- 9}$ in IEEE 754 format.

My comment: Deepseek uses a well known algorithm to convert the mantissa. Step 4. "Adjust the Exponent" with 2^-30 approximates 10^-9 is wrong by nearly 7% and does not include the 2^3 exponent from normalizing the mantissa. I check with a little ANSI C test program:

// tdouble.c #include <stdio.h> #include <stdlib.h> typedef union { double d; unsigned long long l; } FL; int main() { char *s = "9.99e-9"; printf("%s=\n", s); FL x; x.d = atof(s); for (int i = 0; i < 64; ++i) { if (x.l & 0x8000000000000000) { printf("1"); } else { printf("0"); } x.l <<= 1; } printf("\n"); }

The output is:

9.99e-9= 0011111001000101011101000000111110000010001110000010110111100001

The Deepseek output was:

0011111000010011111110101110000101000111101011100001010001111011

Do you see the difference? I say: AI hallucination at its best. Good wording, bad content. Not enough training material or poor quality training material for the AI model for this topic. I don't think ChatGPT performs better. I remember the old saying: everything you test, works, everything you test not, works not.

Contact

My contact E-mail: